
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)若![]() 在区间
在区间![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)切线方程为![]() .
.
(Ⅱ)当![]() 时,
时, ![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]() ;
;
当![]() 时,
时, ![]() 的单调增区间是
的单调增区间是![]() ;
;
当![]() 时,
时,![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]() .
.
(Ⅲ)![]() .
.
【解析】
试题分析:(Ⅰ)切线的斜率,等于在切点的导函数值.
(Ⅱ)通过“求导数,求驻点,讨论各区间导数值的正负”,确定函数的单调区间。本题应特别注意讨论![]() ,
,![]() ,
,![]() 时的不同情况.
时的不同情况.
(Ⅲ)![]() 在区间
在区间![]() 上恒成立,只需
上恒成立,只需![]() 在区间
在区间![]() 的最小值不大于0.
的最小值不大于0.
试题解析:(Ⅰ)因为![]() ,
,![]() ,
,
所以![]() , 1分
, 1分
![]() ,
,![]() , 3分
, 3分
所以切线方程为![]() . 4分
. 4分
(Ⅱ)![]() , 5分
, 5分
由![]() 得
得![]() , 6分
, 6分
当![]() 时,在
时,在![]() 或
或![]() 时
时![]() ,在
,在![]() 时
时![]() ,
,
所以![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]() ; 7分
; 7分
当![]() 时,在
时,在![]() 时
时![]() ,所以
,所以![]() 的单调增区间是
的单调增区间是![]() ; 8分
; 8分
当![]() 时,在
时,在![]() 或
或![]() 时
时![]() ,在
,在![]() 时
时![]() .
.
所以![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ,单调减区间是
,单调减区间是![]() . 10分
. 10分
(Ⅲ)由(Ⅱ)可知![]() 在区间
在区间![]() 上只可能有极小值点,
上只可能有极小值点,
所以![]() 在区间
在区间![]() 上的最大值在区间的端点处取到, 12分
上的最大值在区间的端点处取到, 12分
即有![]() 且
且![]() ,
,
解得![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】指出下列命题是全称量词命题还是存在量词命题,并判断它们的真假.
(1)x∈N,2x+1是奇数;
(2)存在一个x∈R,使![]() =0;
=0;
(3)对任意实数a,|a|>0;
(4)有一个角α,使sinα=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将
,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,有下列叫个结论:
的图象,有下列叫个结论:
![]() 在
在![]() 单调递增;
单调递增; ![]() 为奇函数;
为奇函数;
![]() 的图象关于直线
的图象关于直线![]() 对称;
对称; ![]() 在
在![]() 的值域为
的值域为![]() .
.
其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理﹑化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设![]() 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为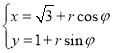 (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
,![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C三地有直道相通,其中AB、BC为步行道,AC为机动车道,已知A在B的正北方向6千米处,C在B的正东方向![]() 千米处,某校开展步行活动,从A地出发,经B地到达C地,中途不休息.
千米处,某校开展步行活动,从A地出发,经B地到达C地,中途不休息.

(1)媒体转播车从A出发,沿AC行至点P处,此时![]() ,求PB的距离;
,求PB的距离;
(2)媒体记者随队步行,媒体转播车从A地沿AC前往C,两者同时出发,步行的速度为6千米/小时,为配合转播,转播车的速度为12千米/小时,记者和转播车通过专用对讲机保持联系,转播车开到C地后原地等待,直到记者到达C地,若对讲机的有效通话距离不超过9千米,求他们通过对讲机能保持联系的总时长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
(1)“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;
互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若![]() ,则
,则![]() 有实数解”的逆否命题;
有实数解”的逆否命题;
(4)“若![]() ,则
,则![]() ”的逆否命题.
”的逆否命题.
其中真命题为( )
A. (1)(2) B. (2)(3) C. (4) D. (1)(2)(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com