


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012届重庆市八中高三第二次月考文科数学 题型:解答题
(本题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
市工商局于今年3月份,对市内流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的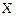 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
(Ⅰ)甲喝两瓶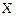 饮料,均合格的概率
饮料,均合格的概率
(Ⅱ)甲、乙、丙每人喝两瓶,恰有一人喝到不合格饮料的概率(精确到0.01)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第二次月考文科数学 题型:解答题
(本题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
市工商局于今年3月份,对市内流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的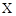 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
(Ⅰ)甲喝两瓶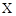 饮料,均合格的概率
饮料,均合格的概率
(Ⅱ)甲、乙、丙每人喝两瓶,恰有一人喝到不合格饮料的概率(精确到0.01)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆八中高三(上)第二次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com