
分析 (1)由题意列关于a,b,c的方程组,求解得到a,b,c的值,则椭圆方程可求;
(2)联立直线方程与椭圆方程,利用根与系数的关系求得A、B中点的坐标,代入圆的方程求得m的值.
解答 解:(1)由题意,得$\left\{\begin{array}{l}{{a}^{2}=2b}\\{{a}^{2}-{b}^{2}={c}^{2}}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\sqrt{2}}\\{b=1}\\{c=1}\end{array}\right.$.
∴椭圆的标准方程为${x}^{2}+\frac{{y}^{2}}{2}=1$;
(2)设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0),
联立$\left\{\begin{array}{l}{x-y+m=0}\\{{x}^{2}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得3x2+2mx+m2-2=0.
则${x}_{1}+{x}_{2}=-\frac{2m}{3}$,${x}_{0}=\frac{{x}_{1}+{x}_{2}}{2}=-\frac{m}{3}$,${y}_{0}={x}_{0}+m=\frac{2m}{3}$.
∴M($-\frac{m}{3},\frac{2m}{3}$).
∵M在圆x2+y2=5上,∴(-$\frac{m}{3}$)2+($\frac{2m}{3}$)2=5,
解得:m=±3.
点评 本题考查椭圆标准方程的求法,考查直线与椭圆位置关系的应用,属中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,b∥β,a∥b,则α∥β | ||
| C. | 若a⊥α,a?β,则α⊥β | D. | 若a,b在α内的射影相互垂直,则a⊥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
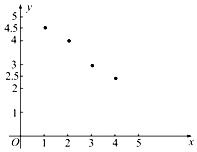 如表是某厂1~4月份用水量(单位:百吨)的一组数据.由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a,则a=( )
如表是某厂1~4月份用水量(单位:百吨)的一组数据.由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a,则a=( )| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 10.5 | B. | 5.15 | C. | 5.2 | D. | 5.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈N,x2-3x+2≤0 | B. | ?x∉N,x2-3x+2≤0 | C. | ?x∈N,x2-3x+2≤0 | D. | ?x∈N,x2-3x+2>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com