本题考查的知识点是直线与平面垂直的性质及用空间向量求平面间的夹角,其中求二面角的值时,一是几何法,关键是找到二面有的平面角,二是向量法,关键是求出两个平面的法向量.
(1)取AD的中点O,连接OP,OE,由等腰三角形三线合一,及OE∥AB,可得OE⊥AD,又由侧面PAD⊥底面ABCD,我们易得到AD⊥平面OPE.再由线面垂直的性质定理可得到AD⊥PE;再证明AD⊥EO
(2)有两种解法,一是取OE的中点F,连接FG,OG,结合(1)的结论,我们易得∠GOE就是二面角E-AD-G的平面角,解三角形GOE即可得到答案;二是建立空间坐标系,确定各个顶点的坐标,及平面ADE及平面ADG的法向量,然后代入向量夹角公式,我们易求出二面角E-AD-G的余弦值,进而求出二面角E-AD-G的正切值.
(1)∵

,∴

,……………………2分
又

是

的中点,∴OE∥AB,∴OE⊥AD. ……………………4分
又OP∩OE=0,∴AD⊥平面OPE. ……………………6分
(2)建立如图所示的空间直角坐标系,则A(1,0,0),D(-1,0,0),P(0,0,),E(0,2,0),



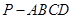 中,侧面
中,侧面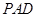 ⊥底面
⊥底面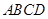 ,底面
,底面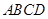 是边长为
是边长为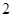 的正方形,又
的正方形,又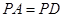 ,
,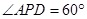 ,
, 分别是
分别是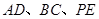 的中点.
的中点.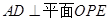 ;
;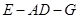 的余弦值.
的余弦值. 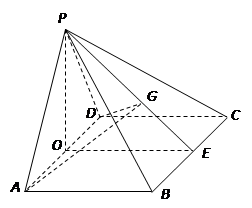

 ,∴
,∴ ,……………………2分
,……………………2分 是
是 的中点,∴OE∥AB,∴OE⊥AD. ……………………4分
的中点,∴OE∥AB,∴OE⊥AD. ……………………4分



 教材全解字词句篇系列答案
教材全解字词句篇系列答案