练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，内角A，B，C所对的边分别是a，b，c.已知a＝2，c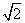＝，cosA＝－.

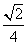    (1)求sinC和b的值；

    (2)求cos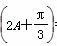的值．


    解：(1)在△ABC中，由cosA＝－，可得sinA＝.

    又由及a＝2，c＝，可得sinC＝.

    由a2＝b2＋c2－2bccosA，得b2＋b－2＝0，

    因为b＞0，故解得b＝1.所以sinC＝，b＝1.

    (2)由cosA＝－，sinA＝，

    得cos2A＝2cos2A－1＝－，

    sin2A＝2sinAcosA＝－.

    所以，cos＝cos2Acos－sin2Asin

    ＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若cosα＝－，α是第三象限的角，则sin(α＋)＝(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知ω＞0，函数f(x)＝sin上单调递减，则ω的取值范围是(　　)

    A.                           B.

    C.                           D．(0,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数y＝Asin(ωx＋φ)＋n的最大值为4，最小值是0，最小正周期是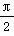，直线x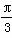＝是其图象的一条对称轴，若A>0，ω>0,0<φ<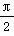，则函数解析式为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C所对边的长分别为a，b，c，若a2＋b2＝2c2，则cosC的最小值为(　　)

    A.                            B.

    C.                              D．－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝cos(x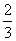＋π)＋2cos2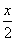，x∈R.

    (1)求f(x)的值域；

    (2)记△ABC的内角A、B、C的对边长分别为a、b、c，若f(B)＝1，b＝1，c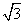＝，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直径为30 m的圆形广场中央上空，设置一个照明光源，射向地面的光呈圆形，且其轴截面顶角为120°，若要光源恰好照亮整个广场，则光源的高度为________ m.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的通项公式为an＝n2－5n＋4.

    (1)数列中有多少项是负数？

    (2)n为何值时，an有最小值？并求出最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对正整数n，设曲线y＝xn(1－x)在x＝2处的切线与y轴交点的纵坐标为an，则数列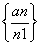的前n项和的公式是(　　)

    A．2n                             B．2n－2

    C．2n＋1                            D．2n＋1－2

    查看答案和解析>>

    同步练习册答案