
【题目】如图,在平面直角坐标系中,点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),锐角α的终边与单位圆O交于点P. (Ⅰ)用α的三角函数表示点P的坐标;
,0),锐角α的终边与单位圆O交于点P. (Ⅰ)用α的三角函数表示点P的坐标;
(Ⅱ)当 ![]()
![]() =﹣
=﹣ ![]() 时,求α的值;
时,求α的值;
(Ⅲ)在x轴上是否存在定点M,使得| ![]() |=
|= ![]() |
| ![]() |恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的横坐标;若不存在,请说明理由.
【答案】解:锐角α的终边与单位圆O交于点P. (Ⅰ)用α的三角函数表示点P的坐标为(cosα,sinα);
(Ⅱ) ![]() ,
, ![]() ,
, ![]()
![]() =﹣
=﹣ ![]() 时,
时,
即(cos ![]() )(cos
)(cos ![]() )+sin2α=
)+sin2α= ![]() ,整理得到cos
,整理得到cos ![]() ,所以锐角α=60°;
,所以锐角α=60°;
(Ⅲ)在x轴上假设存在定点M,设M(x,0), ![]() ,
,
则由| ![]() |=
|= ![]() |
| ![]() |恒成立,得到
|恒成立,得到 ![]() =
= ![]() ,整理得2cosα(2+x)=x2﹣4,
,整理得2cosα(2+x)=x2﹣4,
所以存在x=﹣2时等式恒成立,所以存在M(﹣2,0)
【解析】(Ⅰ)用α的三角函数的坐标法定义得到P 坐标;(Ⅱ)首先写成两个向量的坐标根据 ![]()
![]() =﹣
=﹣ ![]() ,得到关于α的三角函数等式,求α的值;(Ⅲ)假设存在M(x,0),进行向量的模长运算,得到三角等式,求得成立的x值.
,得到关于α的三角函数等式,求α的值;(Ⅲ)假设存在M(x,0),进行向量的模长运算,得到三角等式,求得成立的x值.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,三角形ABC为等腰直角三角形,AC=BC= ![]() ,AA1=1,点D是AB的中点.
,AA1=1,点D是AB的中点. 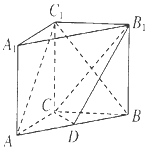
(1)求证:AC1∥平面CDB1;
(2)二面角B1﹣CD﹣B的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在D上的函数y=h(x)在点P(x0 , h(x0))处的切线方程为l:y=g(x),当x≠x0时,若 ![]() >0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=x2﹣6x+4lnx的“类对称点”的横坐标是( )
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=x2﹣6x+4lnx的“类对称点”的横坐标是( )
A.1
B.![]()
C.e
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由
是由![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() .现将
.现将![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]() 的大小为90°,得到图形如图(2)所示,连接
的大小为90°,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(Ⅰ)证明: ![]() ;
;
(Ⅱ)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,若存在常数T≠0,使得f(x)=Tf(x+T)对任意的x∈R成立,则称函数f(x)是Ω函数. (Ⅰ)判断函数f(x)=x,g(x)=sinπx是否是Ω函数;(只需写出结论)
(Ⅱ)说明:请在(i)、(ii)问中选择一问解答即可,两问都作答的按选择(i)计分
(i)求证:若函数f(x)是Ω函数,且f(x)是偶函数,则f(x)是周期函数;
(ii)求证:若函数f(x)是Ω函数,且f(x)是奇函数,则f(x)是周期函数;
(Ⅲ)求证:当a>1时,函数f(x)=ax一定是Ω函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB为圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦AG交CD于F.
(1)求证:E,F,G,B四点共圆;
(2)若GF=2FA=4,求线段AC的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一点在直线上从时刻t=0(s)开始以速度v(t)=t2﹣4t+3(m/s)运动,求:
(1)在t=4s时的位置;
(2)在t=4s的运动路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com