Question

设函数f(x)=（x²+ax+a）e^-x，其中x∈R，a是实常数，e是自然对数的底数．
(Ⅰ)确定a的值，使f(x)的极小值为0；
(Ⅱ)证明：当且仅当a=3时，f（x）的极大值为3；
(Ⅲ)讨论关于x的方程f(x)+f′(x)=2xe^-x+x^-2(x≠0)的实数根的个数．

Answer 1

解：(Ⅰ)，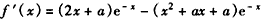
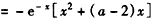令f′(x)=0，解得：x=0或x=2-a，
①当a=2时，f′(x)≤0，此时无极值；
②当0＜2-a，即a＜2时，f′(x)和f(x)的变化如下表1，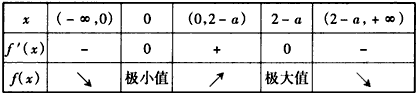

此时应有f(0)=0，所以，a=0＜2；
③当0＞2-a，即a＞2时，f′(x)和f(x)的变化如下表2，

此时应有f(2-a)=0，即，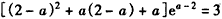
所以必有；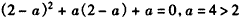
综上所述，当a=0或a=4时，f(x)的极小值为0。
(Ⅱ)若a＜2，则由表1知，应有f(2-a)=3，
即，
∴，
设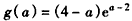，则，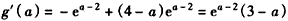
由a＜2，故g′(x)＞0，
于是当a＜2时，g(a)＜g(2)=2＜3，即不可能成立；
若a＞2，则由表2知，应有f(0)=3，即a=3；
综上所述，当且仅当a=3时极大值为3。
(Ⅲ) ∵，
∴方程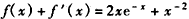可以化为，
进而化为，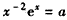
构造函数，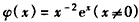
求导可得，，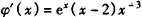
由ψ′(x)＞0得x＜0或x＞2，由ψ′(x)＜0得0＜x＜2，
从而ψ(x)在区间(-∞，0)和(2，+∞)上单调递增，在区间（0，2）上单调递减，
当x=2时，函数ψ(x)取得极小值。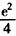
并且结合函数图象可知：当|x|无限趋近于0时，ψ(x)＞0并且取值无限增大，其图象向上无限接近y轴，但永远也达不到y轴（此时y轴足渐近线）；
当x＜0并无限减小时，ψ(x)＞0并且取值也无限减小，其图象在 x轴上方并向左无限接近x轴，但永远也达不到x轴（此时x轴是渐近线）；
当x＞2并无限增大时，ψ(x)＞0并且取值也无增大，其图象在第一象限内向右上方无限延伸（如图所示）
 
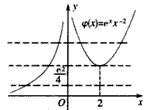
因此，当a≤0时，原方程无实根；
当0＜a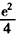＜时，原方程只有一个实数根；
当a=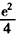时，原方程有两个不等的实数根；
当a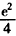＞时，原方程有三个不等的实数根。