
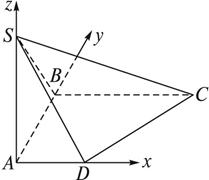
(1)求面SCD与面SBA所成的二面角的正切值;
(2)求SC与平面ABCD所成的角的正弦值.
解:(1)因为AD、AB、AS是三条两两互相垂直的线段,故以A为原点,以AD、AB、AS的方向为x轴、y轴、z轴的正方向建立坐标系,则A(0,0,0)、D(![]() ,0,0)、C(1,1,0)、S(0,0,1),
,0,0)、C(1,1,0)、S(0,0,1),![]() =(
=(![]() ,0,0)是平面SAB的法向量.设面SCD的法向量n=(1,λ,μ),则n·
,0,0)是平面SAB的法向量.设面SCD的法向量n=(1,λ,μ),则n·![]() =(1,λ,μ)·(
=(1,λ,μ)·(![]() ,1,0)=
,1,0)=![]() +λ=0,∴λ=-
+λ=0,∴λ=-![]() .
.

n·![]() =(1,λ,μ)·(-
=(1,λ,μ)·(-![]() ,0,1)=-
,0,1)=-![]() +μ=0,
+μ=0,
∴μ=![]() .
.
∴n=(1,-![]() ,
,![]() ).
).
如以θ表示欲求的二面角,则cos![]() 〈
〈![]() ,n〉,
,n〉,
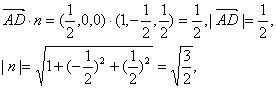
∴cosθ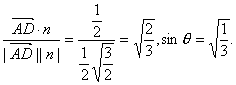
∴tanθ=![]()
∴面SCD与面SBA所成二面角的正切值为![]()
(2)∵![]() 是平面ABCD的法向量,先求
是平面ABCD的法向量,先求![]() 与
与![]() 之间的夹角φ.
之间的夹角φ.
∵![]()
∴![]()
![]()
![]()
∴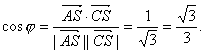 又∵该夹角与直线SC与平面ABCD所成的角互余,
又∵该夹角与直线SC与平面ABCD所成的角互余,
∴所求正弦值为![]() .
.


科目:高中数学 来源: 题型:
(1)求面SCD与面SBA所成的二面角的正切值;
(2)求SC与平面ABCD所成的角的余弦值.
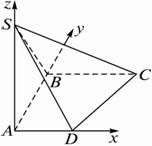
查看答案和解析>>
科目:高中数学 来源: 题型:
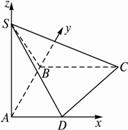
(1)求面SCD与面SBA所成的二面角的正切值;
(2)求SC与平面ABCD所成的角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
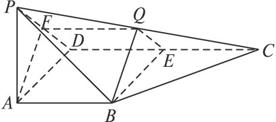
(1)求证:BQ∥平面PAD;
(2)如果点E是线段CD中点,求三棱锥Q—BEC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:

PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
(1)求证:BQ∥平面PAD;
(2)探究在过BQ且与底面ABCD相交的平面中是否存在一个平面α,把四棱锥P—ABCD截成两部分,使得其中一部分为一个四个面都是直角三角形的四面体.若存在,求平面PBC与平面α所成锐二面角的余弦值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com