
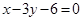 ,若点
,若点 在直线AD上.
在直线AD上.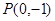 的直线
的直线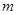 与ABCD外接圆相交于A、B两点,若
与ABCD外接圆相交于A、B两点,若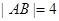 ,求直线m的方程.
,求直线m的方程.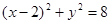 ;(2)
;(2)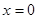 或
或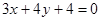 。
。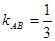 ∴
∴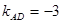
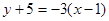 即
即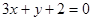 ………2分
………2分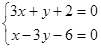 解得
解得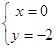 即A(0,-2) ………4分
即A(0,-2) ………4分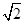 . 故其方程为
. 故其方程为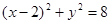 ………6分
………6分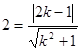 解得:
解得: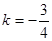
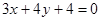
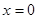 或
或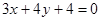 ………12分
………12分

科目:高中数学 来源:不详 题型:解答题
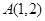 并且在两个坐标轴上的截距的绝对值相等的直线方程
并且在两个坐标轴上的截距的绝对值相等的直线方程查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com