
如图14,在棱长为2的正方体ABCDA1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ.
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
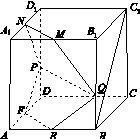
图14
解:方法一(几何方法):
(1)证明:如图①,连接AD1,由ABCDA1B1C1D1是正方体,知BC1∥AD1.
当λ=1时,P是DD1的中点,又F是AD的中点,所以FP∥AD1,所以BC1∥FP.
而FP⊂平面EFPQ,且BC1⊄平面EFPQ,故直线BC1∥平面EFPQ.
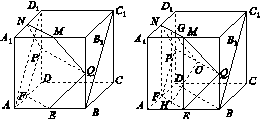
图① 图②
(2)如图②,连接BD.因为E,F分别是AB,AD的中点,所以EF∥BD,且EF= BD.
BD.
又DP=BQ,DP∥BQ,
所以四边形PQBD是平行四边形,故PQ∥BD,且PQ=BD,从而EF∥PQ,且EF= PQ.
PQ.
在Rt△EBQ和Rt△FDP中,因为BQ=DP=λ,BE=DF=1,
于是EQ=FP=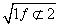 ,所以四边形EFPQ也是等腰梯形.
,所以四边形EFPQ也是等腰梯形.
同理可证四边形PQMN也是等腰梯形.
分别取EF,PQ,MN的中点为H,O,G,连接OH,OG,
则GO⊥PQ,HO⊥PQ,而GO∩HO=O,
故∠GOH是面EFPQ与面PQMN所成的二面角的平面角.
若存在λ,使面EFPQ与面PQMN所成的二面角为直二面角,则∠GOH=90°.
连接EM,FN,则由EF∥MN,且EF=MN知四边形EFNM是平行四边形.
连接GH,因为H,G是EF,MN的中点,
所以GH=ME=2.
在△GOH中,GH2=4,OH2=1+λ2-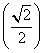
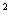 =λ2+
=λ2+ ,
,
OG2=1+(2-λ)2-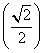
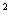 =(2-λ)2+
=(2-λ)2+ ,
,
由OG2+OH2=GH2,得(2-λ)2+ +λ2+
+λ2+ =4,解得λ=1±
=4,解得λ=1±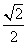 ,
,
故存在λ=1±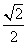 ,使面EFPQ与面PQMN所成的二面角为直二面角.
,使面EFPQ与面PQMN所成的二面角为直二面角.
方法二(向量方法):
以D为原点,射线DA,DC,DD1分别为x,y,z轴的正半轴建立如图③所示的空间直角坐标系.由已知得B(2,2,0),C1(0,2,2),E(2,1,0),F(1,0,0),P(0,0,λ).
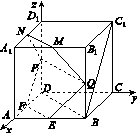
图③
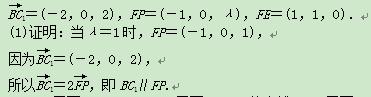 而FP⊂平面EFPQ,且BC1⊄平面EFPQ,故直线BC1∥平面EFPQ.
而FP⊂平面EFPQ,且BC1⊄平面EFPQ,故直线BC1∥平面EFPQ.
(2)设平面EFPQ的一个法向量为n=(x,y,z),则由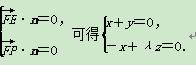
于是可取n=(λ,-λ,1).
同理可得平面MNPQ的一个法向量为m=(λ-2,2-λ,1).
若存在λ,使面EFPQ与面PQMN所成的二面角为直二面角,
则m·n=(λ-2,2-λ,1)·(λ,-λ,1)=0,
即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±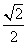 .
.
故存在λ=1±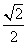 ,使面EFPQ与面PQMN所成的二面角为直二面角.
,使面EFPQ与面PQMN所成的二面角为直二面角.


科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
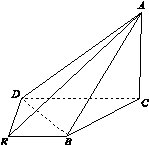
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
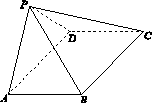
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14所示,在四棱锥P ABCD中,PA⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F AB P的余弦值.
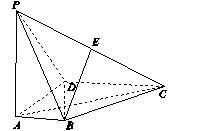
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
已知如图G78所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED⊥平面ABCD,∠BAD= .
.
(1)求证:平面BCF∥平面AED;
(2)若BF=BD=a,求四棱锥ABDEF的体积.
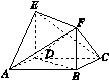
图G78
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人一起到阿里山参观旅游,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后1小时他们同在一个景点的概率是( )
A.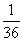 B.
B.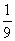
C.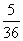 D.
D.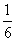
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com