
已知如图G78所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED⊥平面ABCD,∠BAD= .
.
(1)求证:平面BCF∥平面AED;
(2)若BF=BD=a,求四棱锥ABDEF的体积.
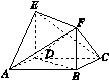
图G78
解:(1)证明:∵四边形ABCD是菱形,
∴BC∥AD.
∵BC⊄平面ADE,AD⊂平面AED,
∴BC∥平面ADE.
又∵四边形BDEF是矩形,∴BF∥DE.
∵BF⊄平面ADE,DE⊂平面ADE,
∴BF∥平面ADE.
∵BC⊂平面BCF,BF⊂平面BCF,且BC∩BF=B,
∴平面BCF∥平面AED.
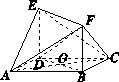
(2)如图,连接AC,AC∩BD=O.
∵四边形ABCD是菱形,
∴AC⊥BD.
又∵ED⊥平面ABCD,AC⊂平面ABCD,∴ED⊥AC.
∵ED,BD⊂平面BDEF,且ED∩BD=D,
∴AC⊥平面BDEF,
∴AO为四棱锥ABDEF的高.
又∵四边形ABCD是菱形,∠BAD= ,
,
∴△ABD为等边三角形.
又∵BF=BD=a,
∴AD=a,AO= a,
a,
∴S四边形BDEF=a2,∴V四棱锥ABDEF=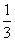 ·a2·
·a2· a=
a= a3.
a3.


科目:高中数学 来源: 题型:
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14,在棱长为2的正方体ABCDA1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ.
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
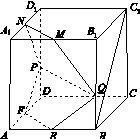
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
一名同学先后投掷一枚骰子两次,第一次向上的点数记为x,第二次向上的点数记为y,在直角坐标系xOy中,以(x,y)为坐标的点落在直线2x+y=8上的概率为( )
A.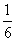 B.
B.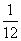
C.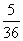 D.
D.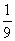
查看答案和解析>>
科目:高中数学 来源: 题型:
下列4个表格中,可以作为离散型随机变量分布列的一个是( )
A.
| X | 0 | 1 | 2 |
| P | 0.3 | 0.4 | 0.5 |
B.
| X | 0 | 1 | 2 |
| P | 0.3 | -0.1 | 0.8 |
C.
| X | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.5 | 0.3 | 0 |
D.
| X | 0 | 1 | 2 |
| P |
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com