
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
解:(1)证明:因为四边形ABCD是等腰梯形,
且AB=2CD,所以AB∥DC,
又M是AB的中点,
所以CD∥MA且CD=MA.
连接AD1.因为在四棱柱ABCD A1B1C1D1中,
CD∥C1D1,CD=C1D1,
所以C1D1∥MA,C1D1=MA,
所以四边形AMC1D1为平行四边形,
因此,C1M∥D1A.
又C1M⊄平面A1ADD1,D1A⊂平面A1ADD1,
所以C1M∥平面A1ADD1.
(2)方法一:连接AC,MC.
由(1)知,CD∥AM且CD=AM,
所以四边形AMCD为平行四边形,
所以BC=AD=MC.
由题意∠ABC=∠DAB=60°,
所以△MBC为正三角形,
因此AB=2BC=2,CA= ,
,
因此CA⊥CB.
设C为坐标原点,建立如图所示的空间直角坐标系C xyz.

所以A( ,0,0),B(0,1,0),D1(0,0,
,0,0),B(0,1,0),D1(0,0, ).
).
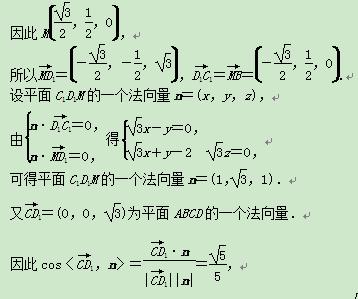 所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为
所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为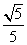 .
.
方法二:由(1)知,平面D1C1M∩平面ABCD=AB,点过C向AB引垂线交AB于点N,连接D1N.
由CD1⊥平面ABCD,可得D1N⊥AB,
因此∠D1NC为二面角C1 AB C的平面角.
在Rt△BNC中,BC=1,∠NBC=60°,
可得CN= ,
,
所以ND1= =
=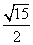 .
.
在Rt△D1CN中,cos∠D1NC=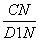 =
=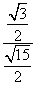 =
=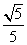 ,
,
所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为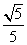 .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
连续掷一枚均匀的正方体骰子(6个面分别标有1,2,3,4,5,6).现定义数列{an}:当向上面上的点数是3的倍数时,an=1;当向上面上的点数不是3的倍数时,an=-1.设Sn是其前n项和,那么S5=3的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
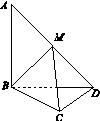
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13所示,四棱锥PABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=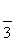 ,M为BC上一点,且BM=
,M为BC上一点,且BM= ,MP⊥AP.
,MP⊥AP.
(1)求PO的长;
(2)求二面角APMC的正弦值.
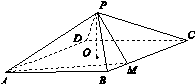
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
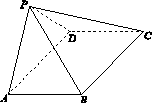
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图14所示,在长方体ABCD A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为Li(i=2,3,4),L1=AE,将线段L1,L2,L3,L4竖直放置在同一水平线上,则大致的图形是( )
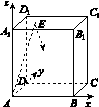
图14
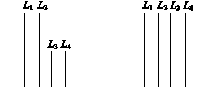
A B
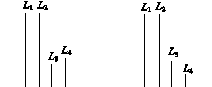
C D
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
已知如图G78所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED⊥平面ABCD,∠BAD= .
.
(1)求证:平面BCF∥平面AED;
(2)若BF=BD=a,求四棱锥ABDEF的体积.
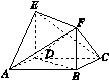
图G78
查看答案和解析>>
科目:高中数学 来源: 题型:
已知平面上的线段l及点P,任取l上一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作d(P,l)
①若点P(1,1),线段l:x﹣y﹣3=0(3≤x≤5),则d(P,l)=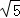 ;
;
②设l是长为2的定线段,则集合D={P|d(P,l)≤1}所表示的图形面积为4;
③若A(1,3),B(1,0),C(﹣1,3),D(﹣1,0),线段l1:AB,l2:CD,则到线段l1,l2距离相等的点的集合D={P|d(P,l1)=d(P,l2)}={(x,y)|x=0};
④若A(﹣1,0),B(1,0),C(0,﹣1),D(0,1),线段l1:AB,l2:CD,则到线段l1,l2距离相等的点的集合D={P|d(P,l1)=d(P,l2)}={(x,y)|x2﹣y2=0}.
其中正确的有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com