
如图14所示,在长方体ABCD A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为Li(i=2,3,4),L1=AE,将线段L1,L2,L3,L4竖直放置在同一水平线上,则大致的图形是( )
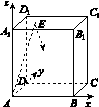
图14
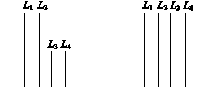
A B
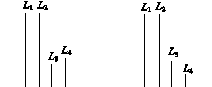
C D
图15
科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
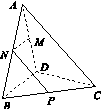
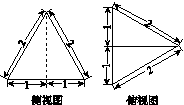
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
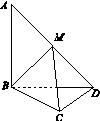
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13所示,在四棱柱ABCD A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.

图13
(1)求证:C1M∥平面A1ADD1;
(2)若CD1垂直于平面ABCD且CD1= ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知棱长为1的正方体ABCD A1B1C1D1中,P,Q是面对角线A1C1上的两个不同的动点.
给出以下四个结论:
①存在P,Q两点,使BP⊥DQ;
②存在P,Q两点,使BP,DQ与直线B1C都成45°的角;
③若PQ=1,则四面体BDPQ的体积一定是定值;
④若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.
以上各结论中,正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
一名同学先后投掷一枚骰子两次,第一次向上的点数记为x,第二次向上的点数记为y,在直角坐标系xOy中,以(x,y)为坐标的点落在直线2x+y=8上的概率为( )
A.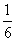 B.
B.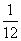
C.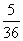 D.
D.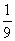
查看答案和解析>>
科目:高中数学 来源: 题型:
有两张卡片,一张的正反面分别写着数字0与1,另一张的正反面分别写着数字2与3,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
A.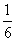 B.
B.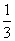
C.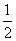 D.
D.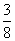
查看答案和解析>>
科目:高中数学 来源: 题型:
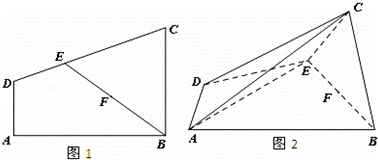
如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,E为CD上一点,且DE=1,EC=2,现沿BE折叠使平面BCE⊥平面ABED,F为BE的中点.图2所示.
(1)求证:AE⊥平面BCE;
(2)能否在边AB上找到一点P使平面ACE与平面PCF所成角的余弦值为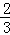 ?若存在,试确定点P的位置,若不存在请说明理由.
?若存在,试确定点P的位置,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com