练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知正四棱台的高是12cm，两底面边长之差为10cm，表面积为512cm2，则下底面的边长为（　　）
    A．10B．12C．14D．16

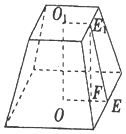
    分析 设OE=xcm，则上底面边长为2xcm，下底面边长为（2x-10）cm，故O1E1=（x-5）cm，结合棱台的全面积为512cm2，解方程可得棱台的上、下底面的边长．

    解答 解：设OE=xcm，则下底面边长为2xcm，上底面边长为（2x-10）cm，故O1E1=（x-5）cm，
    则FE=5cm，
    又∵正四棱台高是12cm，
    ∴EE1=13cm，
    故正四棱台的全面积S=$4{x}^{2}+（2x-10）^{2}+4×\frac{1}{2}×（2x+2x-10）×13$=8（x2+8x-20）=512cm2．
    解得：x=6cm，
    故正四棱台下底面边长为12cm，
    故选B．

    点评 本题考查的知识点是棱台的表面积，考查学生的计算能力，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．已知关于x的方程|2x-a|=1有两个不相等的实数解，则实数a的取值范围是（1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．以下说法正确的有（　　）
    （1）y=x+$\frac{1}{x}$（x∈R）最小值为2；
    （2）a2+b2≥2ab对a，b∈R恒成立；
    （3）a＞b＞0且c＞d＞0，则必有ac＞bd；
    （4）命题“?x∈R，使得x2+x+1≥0”的否定是“?x∈R，使得x2+x+1≥0”；
    （5）实数x＞y是$\frac{1}{x}$＜$\frac{1}{y}$成立的充要条件；
    （6）设p，q为简单命题，若“p∨q”为假命题，则“￢p∨￢q”也为假命题．
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．i是虚数单位，则复数$\frac{5i}{2-i}$的虚部为（　　）
    A．2iB．-2C．2D．-2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知曲线C1：（x-1）2+y2=1与曲线C2：y（y-mx-m）=0，则曲线C2恒过定点（-1，0）；若曲线C1与曲线C2有4个不同的交点，则实数m的取值范围是（-$\frac{\sqrt{3}}{3}$，0）
    ∪（0，$\frac{\sqrt{3}}{3}$） 

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知圆C：x2+y2=4，直线l：y=x+b，若圆C上恰有4个点到直线l的距离都等于1，则b的取值范围是$-\sqrt{2}＜b＜\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知a=2${\;}^{-\frac{1}{3}}}$，b=log2$\frac{1}{3}$，c=log3π，则（　　）
    A．c＞a＞bB．a＞c＞bC．a＞b＞cD．c＞b＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．函数y=$\sqrt{x+1}$+$\frac{1}{3-x}$的定义域是（　　）
    A．{x|x≥-1}B．{x|x＞-1且x≠3}C．{x|x≠-1且x≠3}D．{x|x≥-1且x≠3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在等差数列{an}中，a1=2，a3+a5=8，则a7=（　　）
    A．3B．6C．7D．8

    查看答案和解析>>

    同步练习册答案