练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．在等差数列{an}中，a1=2，a3+a5=8，则a7=（　　）
    A．3B．6C．7D．8

    分析 由题意可得a4=4，进而可得公差d=1，可得a7=a1+6d，代值计算即可．

    解答 解：∵在等差数列{an}中a1=2，a3+a5=8，
    ∴2a4=a3+a5=8，解得a4=4，
    ∴公差d=$\frac{{a}_{4}-{a}_{1}}{4-1}$=$\frac{2}{3}$，
    ∴a7=a1+6d=2+4=6
    故选：B．

    点评 本题考查等差数列的通项公式，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．已知正四棱台的高是12cm，两底面边长之差为10cm，表面积为512cm2，则下底面的边长为（　　）
    A．10B．12C．14D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．不等式log${\;}_{\frac{1}{2}}}$（2x-1）＜log${\;}_{\frac{1}{2}}}$（-x+5）的解集为（2，5）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

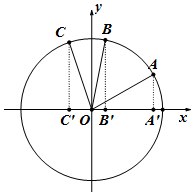    7．如图，在平面直角坐标系中，锐角α、β及角α+β的终边分别与单位圆O交于A，B，C三点．分别作AA'、BB'、CC'垂直于x轴，若以|AA'|、|BB'|、|CC'|为三边长构造三角形，则此三角形的外接圆面积为（　　）
    A．$\frac{π}{4}$B．$\frac{π}{2}$C．$\frac{3π}{4}$D．π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知等差数列{an}的首项和公差都为2，且a1、a8分别为等比数列{bn}的第一、第四项．
    （1）求数列{an}、{bn}的通项公式；
    （2）设cn=$\frac{4}{{（{{log}_2}{b_{n+1}}）{a_n}}}$，求{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．等差数列{an}中，已知前15项的和S15=45，则a8等于 （　　）
    A．$\frac{45}{4}$B．6C．$\frac{45}{8}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

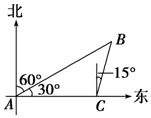    11．如图，一船以每小时20km的速度向东航行，船在A处看到一个灯塔B在北偏东60°方向，行驶4小时后，船到达C处，看到这个灯塔在北偏东15°方向，这时船与灯塔间的距离为$40\sqrt{2}$km．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=（x+a）lnx，g（x）=$\frac{{2{x^2}}}{e^x}$，已知曲线y=f（x）在x=1处的切线过点（2，3）．
    （1）求实数a的值．
    （2）是否存在自然数k，使得函数y=f（x）-g（x）在（k，k+1）内存在唯一的零点？如果存在，求出k；如果不存在，请说明理由．
    （3）设函数h（x）=min{f（x），g（x）}，（其中min{p，q}表示p，q中的较小值），对于实数m，?x0∈（0，+∞），使得h（x0）≥m成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．计算下列各式：
    （1）（$\root{3}{25}$-$\sqrt{125}$）÷$\root{4}{5}$；
    （2）$\frac{{a}^{2}}{\sqrt{a}•\root{3}{{a}^{2}}}$ （a＞0）．

    查看答案和解析>>

    同步练习册答案