
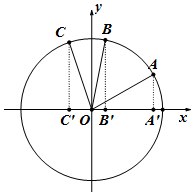
 如图,在平面直角坐标系中,锐角α、β及角α+β的终边分别与单位圆O交于A,B,C三点.分别作AA'、BB'、CC'垂直于x轴,若以|AA'|、|BB'|、|CC'|为三边长构造三角形,则此三角形的外接圆面积为( )
如图,在平面直角坐标系中,锐角α、β及角α+β的终边分别与单位圆O交于A,B,C三点.分别作AA'、BB'、CC'垂直于x轴,若以|AA'|、|BB'|、|CC'|为三边长构造三角形,则此三角形的外接圆面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
分析 由题意可求三角形的三边长为sinα、sinβ、sin(α+β),设边长为sin(α+β)的所对的三角形内角为θ,由余弦定理,三角函数恒等变换的应用化简可得cosθ=-cos(α+β),结合角的范围利用同角三角函数基本关系式可求sinθ,利用正弦定理可求三角形外接圆的半径,利用圆的面积公式即可得解.
解答 (本题满分为12分)
解:由题意可得:|AA'|=sinα、|BB'|=sinβ、|CC'|=sin(α+β),
设边长为sin(α+β)的所对的三角形内角为θ,
则由余弦定理可得,cosθ=$\frac{si{n}^{2}α+si{n}^{2}β-si{n}^{2}(α+β)}{2sinαsinβ}$
=$\frac{si{n}^{2}α+si{n}^{2}β-(sinαcosβ)^{2}-(cosαsinβ)^{2}}{2sinαsinβ}$-cosαcosβ
=$\frac{si{n}^{2}α(1-co{s}^{2}β)+si{n}^{2}β(1-co{s}^{2}α)}{2sinαsinβ}$-cosαcosβ
=sinαsinβ-cosαcosβ
=-cos(α+β),
∵α,β∈(0,$\frac{π}{2}$)
∴α+β∈(0,π)
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=sin(α+β)
设外接圆的半径为R,则由正弦定理可得2R=$\frac{sin(α+β)}{sin(α+β)}$=1,
∴R=$\frac{1}{2}$,
∴外接圆的面积S=πR2=$\frac{π}{4}$.
故选:A.
点评 本题主要考查了余弦定理,三角函数恒等变换的应用,同角三角函数基本关系式,正弦定理,圆的面积公式在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-1} | B. | {x|x>-1且x≠3} | C. | {x|x≠-1且x≠3} | D. | {x|x≥-1且x≠3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com