
分析 (1)分别算出房子的两个侧面积乘以20再加上房子的正面面积乘以40再加上屋顶和地面的造价即为总造价;
(2)我们可以先求房屋总造价的函数解析式,利用基本不等式即可求出函数的最小值,进而得到答案.
解答 解:(1)$y=2×(2x×20+40×\frac{36}{x})+1800$…(4分)
=$80(x+\frac{36}{x})+1800(0<x≤7)$…(5分)
定义域是(0,7]…(6分)
(2)∵$x+\frac{36}{x}≥2\sqrt{36}=12$,…(9分)
当且仅当$x=\frac{36}{x}$即x=6时取=…(10分)
∴y≥80×12+1800=2760…(11分)
答:当侧面长度x=6时,总造价最低为2760元.…(12分)
点评 本题考查函数模型的构建,考查基本不等式的运用,考查分类讨论的数学思想,正确构建函数是关键,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $0≤a≤\frac{1}{5}$ | B. | $a≤\frac{1}{5}$ | C. | a≥-3 | D. | $a≤\frac{1}{5}$或0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
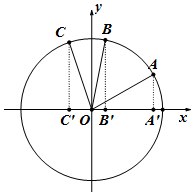 如图,在平面直角坐标系中,锐角α、β及角α+β的终边分别与单位圆O交于A,B,C三点.分别作AA'、BB'、CC'垂直于x轴,若以|AA'|、|BB'|、|CC'|为三边长构造三角形,则此三角形的外接圆面积为( )
如图,在平面直角坐标系中,锐角α、β及角α+β的终边分别与单位圆O交于A,B,C三点.分别作AA'、BB'、CC'垂直于x轴,若以|AA'|、|BB'|、|CC'|为三边长构造三角形,则此三角形的外接圆面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{45}{4}$ | B. | 6 | C. | $\frac{45}{8}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
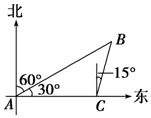 如图,一船以每小时20km的速度向东航行,船在A处看到一个灯塔B在北偏东60°方向,行驶4小时后,船到达C处,看到这个灯塔在北偏东15°方向,这时船与灯塔间的距离为$40\sqrt{2}$km.
如图,一船以每小时20km的速度向东航行,船在A处看到一个灯塔B在北偏东60°方向,行驶4小时后,船到达C处,看到这个灯塔在北偏东15°方向,这时船与灯塔间的距离为$40\sqrt{2}$km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧q | D. | ¬p∨q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com