练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】我国古代数学家刘徽在《九章算术注》中提出割圆术：“割之弥细，所失弥少，割之割，以至于不可割，则与圆合体，而无所失矣”，即通过圆内接正多边形细割圆，并使正多边形的面积无限接近圆的面积，进而来求得较为精确的圆周率.如果用圆的内接正边形逼近圆，算得圆周率的近似值记为，那么用圆的内接正边形逼近圆，算得圆周率的近似值加可表示成（ ）

    A.B.C.D.

    【答案】C

    【解析】

    设圆的半径为，由内接正边形的面积无限接近圆的面积可得：，由内接正边形的面积无限接近圆的面积可得：，问题得解.

    设圆的半径为，将内接正边形分成个小三角形，

    由内接正边形的面积无限接近圆的面积可得：

    ，整理得：，

    此时，即：

    同理，由内接正边形的面积无限接近圆的面积可得：

    ，整理得：

    此时

    所以

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为的学生成绩样本，得频率分布表如下：

    组号

    分组

    频率

    频数

    第一组

    第二组

    ①

    第三组

    ②

    第四组

    第五组

    合计

    （1）写出表中①、②位置的数据；

    （2）估计成绩不低于分的学生约占多少；

    （3）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取名学生进行第二轮考核，分别求第三、四、五各组参加考核的人数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在中，，，，分别是，，中点，，.现将沿折起，如图2所示，使二面角为，是的中点.

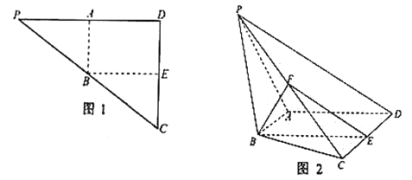
    （1）求证：面面；

    （2）求直线与平面所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知是递增数列，其前项和为，，且，．

    （Ⅰ）求数列的通项；

    （Ⅱ）是否存在使得成立？若存在，写出一组符合条件的的值；若不存在，请说明理由；

    （Ⅲ）设，若对于任意的，不等式

    恒成立，求正整数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为选拔参加“央视猜灯谜大赛”的队员，在校内组织猜灯谜竞赛．规定：第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛．现有200名学生参加知识测试，并将所有测试成绩绘制成如下所示的频率分布直方图．
    （Ⅰ）估算这200名学生测试成绩的中位数，并求进入第二阶段比赛的学生人数；
    （Ⅱ）将进入第二阶段的学生分成若干队进行比赛．现甲、乙两队在比赛中均已获得120分，进入最后抢答阶段．抢答规则：抢到的队每次需猜3条谜语，猜对1条得20分，猜错1条扣20分．根据经验，甲队猜对每条谜语的概率均为 ，乙队猜对前两条的概率均为 ，猜对第3条的概率为 ．若这两队抢到答题的机会均等，您做为场外观众想支持这两队中的优胜队，会把支持票投给哪队？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx+1．
    （Ⅰ）证明：当x＞0时，f（x）≤x；
    （Ⅱ）设 ，若g（x）≥0对x＞0恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某保险公司开设的某险种的基本保费为万元，今年参加该保险的人来年继续购买该险种的投保人称为续保人，续保人的下一年度的保费与其与本年度的出险次数的关联如下：

    本年度出险次数

    下一次保费（单位：万元）

    设今年初次参保该险种的某人准备来年继续参保该险种，且该参保人一年内出险次数的概率分布列如下：

    一年内出险次数

    概率

    （）求此续保人来年的保费高于基本保费的概率．

    （）若现如此续保人来年的保费高于基本保费，求其保费比基本保费高出的概率．

    （）求该续保人来年的平均保费与基本保费的比值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4﹣4：极坐标与参数方程
    极坐标系与直角坐标系xOy有相同的长度单位，以原点O为极点，以x轴正半轴为极轴．已知曲线C1的极坐标方程为 ，曲线C2的极坐标方程为ρsinθ=a（a＞0），射线 ， 与曲线C1分别交异于极点O的四点A，B，C，D．
    （Ⅰ）若曲线C1关于曲线C2对称，求a的值，并把曲线C1和C2化成直角坐标方程；
    （Ⅱ）求|OA||OC|+|OB||OD|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex﹣1﹣ax（a＞1）在[0，a]上的最小值为f（x0），且x0＜2，则实数a的取值范围是（ ）
    A.（1，2）
    B.（1，e）
    C.（2，e）
    D.（ ，+∞）

    查看答案和解析>>

    同步练习册答案