
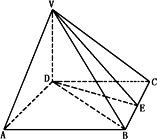
如图,四棱锥的高为h,底面为菱形,侧面VDA和侧面VDC所成的二面角为120°,且都垂直于底面,另两个侧面与底面所成的角都是45°,求此棱锥的全面积.
|
解:由已知条件可得VD⊥底面ABCD,VD⊥DA,VD⊥DC, ∴∠ADC=120°. ∵ABCD为菱形, ∴BD是∠ADC的平分线. ΔADB和ΔDBC是全等的等边三角形,取BC的中点E, 连DE,BC⊥DE,BC⊥VE,∴∠VED=45°. 在直角ΔDEC中,EC=DE·ctg60°= ∴S底=BC·DE= SΔVBC=SΔVAB= SΔVAD=SΔVDC= ∴S全= = 解析:由面面垂直的性质可证得VD⊥底面,因为SΔVDA=SΔVDC,∠ADC=120°,DB是其平分线,而SΔVBC=SΔVAB,所以全面积不难求得. 评析:本题的关键是侧面VDA和侧面VDC都垂直于底面,则它们的交线VD⊥底面ABCD,从而∠ADC=120°. |


科目:高中数学 来源: 题型:
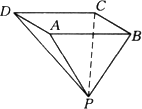
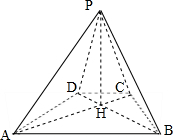 如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高.
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高.| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
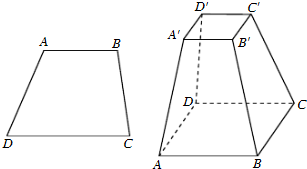 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.| x |
| x+h |
| a |
| b |
| ah |
| b-a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| h |
| y-a |
| b-a |
| b-a |
| h |
| ∫ | h 0 |
| b-a |
| h |
| b-a |
| 2h |
| | | h 0 |
| b-a |
| 2h |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
用一块钢锭浇铸一个度均匀且全面积为2 m2的正四棱锥形有盖容器(如图),设容器的高为h m,盖子边长为a m.
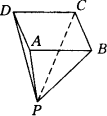
(1)求a关于h的函数解析式.
(2)设容器的容积为V m3,则当h为何值时,V最大?求出V的最大值.(求解本题时,不计容器的厚度)
查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
用一块钢锭浇铸一个厚度均匀,且全面积为2平方米的正四棱锥形有盖容器(如图),设容器的高为h米,盖子边长为a米.
(1)求a关于h的函数解析式.
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值(不计容器的厚度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com