练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．某质检部门要检验一批乳制品是否合格，从待抽检的500待乳制品中抽取40待进行检验，利用随机数表抽取样本时，先将500待乳制品按000，001，…，499进行标号，如果从以下随机数表第2行第3列的数考试向右读，则得到的第5个样本的编号是350

    分析 找到第7行第8列的数开始向右读，确定符合条件的数，即可得出结论．

    解答 解：找到第2行第3列的数开始向右读，第一个符合条件的是421，
    第二个数是315，
    第三个数是474，
    第四个数是476，
    第五个数是350，
    故答案为：350．

    点评 抽样方法，随机数表的使用，考生不要忽略．在随机数表中每个数出现在每个位置的概率是一样的，所以每个数被抽到的概率是一样的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

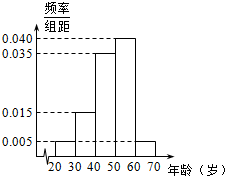    16．跳广场舞是现在广大市民喜爱的户外健身运动，某健身运动公司为了解本地区市民对跳广场舞的热衷程度，随机抽取了100名跳广场舞的市民，统计其年龄（单位：岁）并整理得到如下的频率分布直方图（其中年龄的分组区间分别为[20，30），[30，40），[40，50），[50，60），[60，70]），其中女性市民有55名，将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”．已知其中有30名女性广舞迷．
    （1）根据已知条件完成下面的2×2列联表，能否在犯错误的概率不超过0.05的前提下认为广舞迷与性别有关？
     广舞迷非广舞迷合计
    男   
    女   
    合计   
    （2）将所抽样本中不小于60岁的广舞迷称为“超级广舞迷”，现从广舞迷中随机抽出2名市民，求其中超级广舞迷人数的分布列与期望．
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$；
    P（K2≥k0）0.050.0250.0100.005
     k03.8415.0246.6357.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数f（x）=ax3+bx+4（a，b∈R），f（lg（log210））=5，则f（lg（lg2））=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

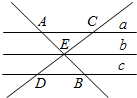    14．如图所示，a∥b∥c，直线AB与a、b、c分别相交于A、E、B，直线CD与a、b、c分别相交于C、E、D，AE=EB，则有（　　）
    A．AE=CEB．BE=DEC．CE=DED．CE＞DE

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若函数f（x）=3x-1+$\frac{k}{3^x}$为偶函数，则实数k的值为$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．函数y=2sin（$\frac{π}{3}x+1$）的最小正周期是6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知f（x）=x2+2xf′（1）-6，则f′（1）等于（　　）
    A．4B．-2C．0D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

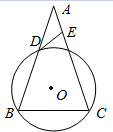    15．如图，圆O的半径为2，等腰△ABC的底边的两端点B，C在圆O上，AB与圆O交于点D，AD=2，圆O的切线DE交AC于E点．
    （I）求证：DE⊥AC；
    （Ⅱ）若∠A=30°，求BD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．椭圆C：$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点为F1，F2，有下列研究问题及结论：
    ①曲线$\frac{x^2}{25-k}+\frac{y^2}{9-k}={1_{\;}}（k＜9）$与椭圆C的焦点相同；
    ②双曲线的焦点是椭圆C 的长轴的端点，顶点是椭圆C的焦点，则其标准方程为$\frac{x^2}{16}-\frac{y^2}{9}=1$；
    ③若点P为椭圆上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$，则$|{\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}}|$=8．
    ④过椭圆C的右焦点F2且斜率为k（k＞0）的直线与C相交于A、B两点．若$\overrightarrow{AF}=3\overrightarrow{FB}$，则k=$\frac{5}{6}$．
    则以上研究结论正确的序号是①②③．

    查看答案和解析>>

    同步练习册答案