练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下列推理过程是演绎推理的是                                          

    A．由平面三角形的性质推测空间三棱锥的性质

    B．某校高二1班有55人，2班有52人，由此得高二所有班人数都超过50人

    C．两条直线平行，同位角相等；若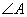与是两条平行直线的同位角，则

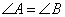
    D．在数列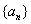中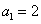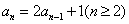，，，由此归纳出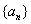的通项公式


     C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    直线y=﹣x+1的倾斜角为（　　）

    　

    A．

    30°

    B．

    45°

    C．

    135°

    D．

    150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l：x﹣y+1=0和点A（1，0）

    （Ⅰ）过点A作直线l的垂线，垂足为B，求点B的坐标；

    （Ⅱ）若直线l与x轴的交点为C，将△ABC绕直线l旋转一周，求所得几何体的表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，⊙O上一点C在直径AB上的射影为D，AC=4，AD=2，则⊙O的面积是　_________　．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A、B、C的对边分别为a、b、c，且角A、B都是锐角，a=6，b=5，sinB=．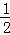

    （1）求sinA和cosC的值；

    （2）设函数f（x）=sin（x+2A），求f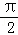（）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一门高射炮射击一次击中目标的概率是0.4，那么至少需要这样的高射炮多少门同时对某一目标射击一次，才能使该目标被击中的概率超过96%（提供的数据：）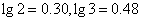                                           

    A.5            B.6            C.7             D.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数在内有极大值，则实数的取值范围是

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用半径为的圆形铁皮剪出一个圆心角为的扇形，制成一个圆锥形容器，要使容器的容积最大，扇形的圆心角                                       

       A.          B.          C.           D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设等差数列 满足：，公差．若当且仅当时，数列的前项和取得最大值，则首项的取值范围是（     ）

    A．       B．      C．        D．

    查看答案和解析>>

    同步练习册答案