练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知函数y=x2-2011x+2012与x轴的交点坐标是（m，0）、（n，0），则（m2-2012m+2012）（n2-2012n+2012）的值为（　　）
    A．2011B．20122C．2011×2012D．2012

    分析 将x=m，n代入函数的表达式，求出m2-2011m+2012=0，n2-2011n+2012=0，再代入求出积即可．

    解答 解：∵函数y=x2-2011x+2012与x轴交点是（m，0），（n，0），
    ∴m，n是方程x2-2011x+2012=0的两个根，
    即m2-2011m+2012=0，n2-2011n+2012=0，
    ∴mn=2012，
    （m2-2012m+2012）（n2-2012n+2012）
    =（m2-2011m+2012-m）（n2-2011n+2012-n）
    =mn
    =2012．
    故选：D．

    点评 本题考查了二次函数的性质，考查韦达定理，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．函数f（x）=ax（a＞0，且a≠1），若f（3a）＞$\sqrt{a}$，则实数a的取值范围为（　　）
    A．（0，$\frac{1}{2}$）∪（1，+∞）B．（0，$\frac{1}{2}$）∪（1，2）C．（0，$\frac{1}{6}$）∪（1，+∞）D．（0，$\frac{1}{6}$）∪（1，6）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知3a=5b=c，且$\frac{1}{a}$+$\frac{1}{b}$=2，求c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．若函数f（x）=$\frac{（2-m）x}{{x}^{2}+m}$的图象如图所示，则m的取值范围是（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．数列{an}的前n项和为Sn=n2+n+1，bn=（-1）nan，n∈N*则数列{bn}的前50项的和为55．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．50名同学参加夏令营活动，需要同时搭建可容纳3人和4人的两种帐篷，使帐篷恰好能容纳所有同学，则有效搭建方案共有4种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．某运动员每次投篮的命中率为60%，现采用随机模拟的方法估计该运动员3次投篮恰好命中2次的概率，先由计算器产生0到9之间取整数值的随机表，指定1，2，3，4表示命不中，5，6，7，8，9，0表示命中，再以每3个随机数为一组，代表3次投篮的结果，经随机模拟产生了如下10组随机数：
    907  966  191  925  271  932  812  458  569  683
    据此估计，该运动员3次投篮恰好命中2次的概率为（　　）
    A．0.35B．0.30C．0.6D．0.70

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．为了了解泉州市新装修房屋室内甲醛含量是否合格，某检测单位随机抽取了20户新装修的房屋进行检测，得到如下结果：（单位：mg/m3）
    A0.02   0.03   0.03   0.04   0.05   0.05   0.05   0.06   0.06   0.06
    A0.06   0.07   0.07   0.08   0.09   0.10   0.10   0.11   0.13   0.14
    （Ⅰ）完成下列表格
    分组频数频率
    [0.00，0.04]40.2
    （0.04，0.08]100.5
    （0.08，0.12]40.2
    （0.12，0.16]20.1
    （Ⅱ）参照测量条件与国家相关标准，空气中甲醛含量不超过0.08mg/m3的房屋可认定为“空气质量合格”，否则为“空气质量不合格”．若检测单位从“空气质量不合格”的房屋户主中随机抽取2名进行访谈，求所选中的两户房屋空气中，甲醛含量均在（0.08，0.12]的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

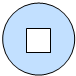    17．欧阳修《卖油翁》中写到：“（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿”．可见“行行出状元”，卖油翁的技艺让人叹为观止，如右图铜钱是直径为4cm的圆形，正中间有边长为1cm的正方形孔，若随机向铜钱上滴一滴油（油滴是直径为0.2cm的球），记“油滴不出边界”为事件A，“油滴整体正好落入孔中”为事件B．则P（B|A）=$\frac{64}{361π}$（不作近似值计算）．

    查看答案和解析>>

    同步练习册答案