
【题目】已知函数f(x)=Asin(ωx+)(其中A>0,||< ![]() ,ω>0)的图象如图所示,
,ω>0)的图象如图所示, 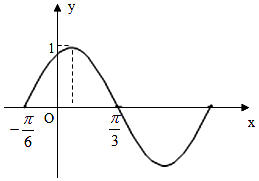
(1)求函数f(x)的解析式;
(2)若关于x的方程f(x)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x﹣k=0在[0,
sin2x﹣k=0在[0, ![]() ]上只有一解,求k的取值范围.
]上只有一解,求k的取值范围.
【答案】
(1)解:∵函数f(x)的最大值为1,A>0,
∴A=1,
又∵函数的周期T=2×[ ![]() ﹣(﹣
﹣(﹣ ![]() )]=π,
)]=π,
∴ω= ![]() =
= ![]() =2,
=2,
∴函数图象经过点P( ![]() ,0),即:sin(2×
,0),即:sin(2× ![]() +)=0,可得:2×
+)=0,可得:2× ![]() +=kπ,k∈Z,解之得:=kπ﹣
+=kπ,k∈Z,解之得:=kπ﹣ ![]() ,k∈Z,
,k∈Z,
∵||< ![]() ,
,
∴解得:= ![]() ,
,
∴函数的表达式为:f(x)=sin(2x+ ![]() )
)
(2)解:∵f(x)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x﹣k=0,
sin2x﹣k=0,
∴sin(2x+ ![]() )+
)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x﹣k=0,化简可得:2cos(2x+
sin2x﹣k=0,化简可得:2cos(2x+ ![]() )=k,
)=k,
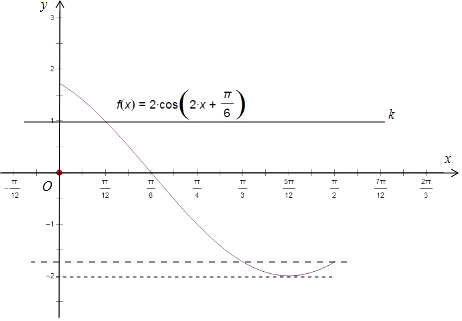
由题意可得函数g(x)=2cos(2x+ ![]() ) 与直线y=k在[0,
) 与直线y=k在[0, ![]() ]上只有一解,
]上只有一解,
由于x∈[0, ![]() ],故2x+
],故2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
故g(x)=2cos(2x+ ![]() )∈[﹣2,
)∈[﹣2, ![]() ].
].
![]() ,
, ![]() ]∪{﹣2}
]∪{﹣2}
【解析】(1)根据函数的最值得到A,再由函数的周期,结合周期公式得到ω的值,再根据函数图象经过点P( ![]() ,0),结合范围||<
,0),结合范围||< ![]() ,解得的值,从而得到函数的表达式.(2)由题意可知函数g(x)=2cos(2x+
,解得的值,从而得到函数的表达式.(2)由题意可知函数g(x)=2cos(2x+ ![]() ) 与直线y=k在[0,
) 与直线y=k在[0, ![]() ]上只有一解,结合余弦函数的图象和性质可得k的取值范围.
]上只有一解,结合余弦函数的图象和性质可得k的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x+ ![]() )﹣1, (Ⅰ)求f(x)的单调递增区间
)﹣1, (Ⅰ)求f(x)的单调递增区间
(Ⅱ)若sin2x+af(x+ ![]() )+1>6cos4x对任意x∈(﹣
)+1>6cos4x对任意x∈(﹣ ![]() ,
, ![]() )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的定义域为(﹣a,0)∪(0,a)(0<a<1),其图象上任意一点P(x,y)满足x2+y2=1,则给出以下四个命题:①函数y=f(x)一定是偶函数;②函数y=f(x)可能是奇函数;③函数y=f(x)在(0,a)上单调递增④若函数y=f(x)是偶函数,则其值域为(a2 , 1)其中正确的命题个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线E上任意一点P到两个定点 ![]() 和
和 ![]() 的距离之和为4,
的距离之和为4,
(1)求动点P的方程;
(2)设过(0,﹣2)的直线l与曲线E交于C、D两点,且 ![]() (O为坐标原点),求直线l的方程.
(O为坐标原点),求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的袋子中装有![]() 个形状相同的小球,分别标有不同的数字
个形状相同的小球,分别标有不同的数字![]() ,现从袋中随机摸出
,现从袋中随机摸出![]() 个球,并计算摸出的这
个球,并计算摸出的这![]() 个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验.记
个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验.记![]() 事件为“数字之和为
事件为“数字之和为![]() ”.试验数据如下表:
”.试验数据如下表:

(1)如果试验继续下去,根据上表数据,出现“数字之和为![]() ”的频率将稳定在它的概率附近.试估计“出现数字之和为
”的频率将稳定在它的概率附近.试估计“出现数字之和为![]() ”的概率,并求
”的概率,并求![]() 的值;
的值;
(2)在(1)的条件下,设定一种游戏规则:每次摸![]() 球,若数字和为
球,若数字和为![]() ,则可获得奖金
,则可获得奖金![]() 元,否则需交
元,否则需交![]() 元.某人摸球
元.某人摸球![]() 次,设其获利金额为随机变量
次,设其获利金额为随机变量![]() 元,求
元,求![]() 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”,“生二孩能休多久产假”等问题成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用![]() 表示两种方案休假周数之和.求随机变量
表示两种方案休假周数之和.求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公车私用、超编配车等现象一直饱受诟病,省机关事务管理局认真贯彻落实党中央、国务院有关公务用车配备使用管理办法,积极推进公务用车制度改革.某机关单位有车牌尾号为2的汽车A和尾号为6的汽车B,两车分属于两个独立业务部门.为配合用车制度对一段时间内两辆汽车的用车记录进行统计,在非限行日,A车日出车频率0.6,B车日出车频率0.5,该地区汽车限行规定如下:
车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且A,B两车出车情况相互独立.
(1)求该单位在星期一恰好出车一台的概率;
(2)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com