
分析 由题意可知:$a<\frac{2lnx-x}{x}$.设$f(x)=\frac{2lnx-x}{x}({x>0})$,?原命题等价于a<f(x)max,求导根据函数的单调性,求得f(x)最大值,即可求得a的取值范围,由椭圆的离心率公式求得椭圆的离心率取值范围,根据不等式的性质,求得a的取值范围,由(?p)∨(?q)为假命题,即p真q真,即可求得实数a的取值范围.
解答 解:命题p:2lnx-x>ax,分参得$a<\frac{2lnx-x}{x}$.
设$f(x)=\frac{2lnx-x}{x}({x>0})$,?x∈(0,+∞),2lnx-x>ax成立,等价于a<f(x)max,
${f^/}(x)=\frac{{2({1-lnx})}}{x^2}$,当0<x<e时,f′(x)>0;
当x>e时,f′(x)<0,
故函数f(x)在(0,e)单调递增,在(2,+∞)单调递减,
∴f(x)max=f(e)=$\frac{2}{e}$-1,
故a<$\frac{2}{e}$-1,①
命题q,双曲线x2+$\frac{y^2}{a}$=1的离心率e∈(1,2),可知a<0,离心率e=$\sqrt{1-a}$,
∵$1<\sqrt{1-a}<2$,
∴-3<a<0. ②…(10分)
若(?p)∨(?q)为假命题,则p真q真,
结合①和②知,$-3<a<\frac{2}{e}-1$…(12分)
点评 本题考查考查简单的逻辑连接词的应用,考查利用导数研究函数的单调性及最值,双曲线的简单性质,考查分离参数法及构造法求未知数的取值范围,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (2,4) | C. | (3,5) | D. | (4,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | 0 | D. | $\frac{{5\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
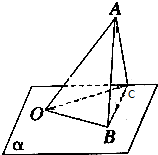 如图所示,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.
如图所示,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
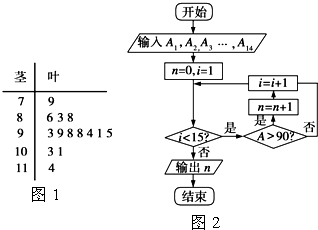 如图1是某高三学生进入高中-二年来的数学考试成绩茎叶图,第1次到第 14次.考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是10.
如图1是某高三学生进入高中-二年来的数学考试成绩茎叶图,第1次到第 14次.考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com