
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在
,若存在![]() ,使
,使![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 型函数”;若存在
型函数”;若存在![]() ,使
,使![]() 恒成立,则称
恒成立,则称![]() 为“
为“![]() 型函数”.已知函数
型函数”.已知函数![]() .
.
(1)设函数![]() .若
.若![]() ,且
,且![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围;
的取值范围;
(2)设函数![]() .证明:当
.证明:当![]() ,
,![]() 为“
为“![]() (1)型函数”;
(1)型函数”;
(3)若![]() ,证明存在唯一整数
,证明存在唯一整数![]() ,使得
,使得![]() 为“
为“![]() 型函数”.
型函数”.
【答案】(1)![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)将![]() 代入,依题意,即
代入,依题意,即![]() 恒成立,设
恒成立,设![]() ,求出函数
,求出函数![]() 的最小值即可得解;
的最小值即可得解;
(2)分析可知,即证![]() ,令
,令![]() ,
,![]() ,方法一:由不等式的性质可知
,方法一:由不等式的性质可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() ,即得证;方法二:令
,即得证;方法二:令![]() ,再对函数
,再对函数![]() 求导,可得当
求导,可得当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,进而得到
,进而得到![]() 的单调性,由此得证;
的单调性,由此得证;
(3)问题等价于证明存在唯一整数![]() ,
,![]() 恒成立,易知当
恒成立,易知当![]() 及
及![]() 时,不合题意,故只需证明
时,不合题意,故只需证明![]() 时符合题意即可,方法一:记
时符合题意即可,方法一:记![]() ,分当
,分当![]() 或
或![]() 以及当
以及当![]() 时证明即可;
时证明即可;
方法二:记![]() ,利用导数求其最大值小于0即可得证.
,利用导数求其最大值小于0即可得证.
(1)![]() 时,
时,![]() .
.
因为![]() 为“
为“![]() 型函数”,
型函数”,
所以![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
设![]() ,则
,则![]() 恒成立,
恒成立,
所以![]() 在
在![]() ,
,![]() 上单调递减,
上单调递减,
所以![]() (1)
(1)![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() ;
;
(2)证明:当![]() 时,要证
时,要证![]() 为“
为“![]() (1)型函数”,
(1)型函数”,
即证![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() ,
,
方法一:当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() ;
;
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
则![]() (1),又
(1),又![]() (1)
(1)![]() ,所以
,所以![]() ,
,
所以![]() 为“
为“![]() (1)型函数”.
(1)型函数”.
方法二:令![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增,又
上单调递增,又![]() (1)
(1)![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
以下同方法一.
(3)证明:函数![]() 为“
为“![]() 型函数”等价于
型函数”等价于![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,
方法一:![]() ,
,
①当![]() 或
或![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,由(2)知
,由(2)知![]() ,
,
所以![]() ,
,
综上,存在唯一整数![]() ,使得
,使得![]() 为“
为“![]() 型函数”.
型函数”.
方法二:![]() ,
,![]() ,
,
记![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
易得![]() ,
,
所以![]() ;
;
又因为![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,
,
且![]() 为
为![]() 的最大值点,
的最大值点,
所以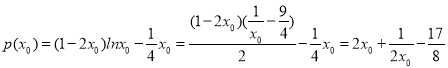 ,
,
注意到![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() .
.
综上,存在唯一整数![]() ,使得
,使得![]() 为“
为“![]() 型函数”.
型函数”.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】用一个平行于底面的截面去截一个正棱锥,截面和底面间的几何体叫正棱台.如图,在四棱台![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
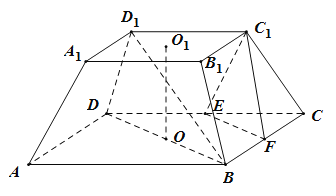
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若侧棱所在直线与上下底面中心的连线![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在
,点E在![]() 上,且
上,且![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() (如图2).
(如图2).
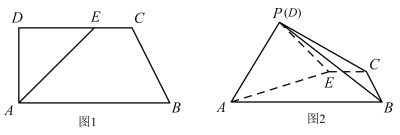
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)在线段![]() 上存在点F,满足
上存在点F,满足![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形(如图所示),为使占地面积最大,则等腰三角形的底角为( )
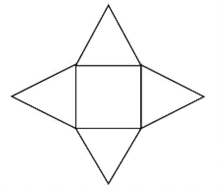
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻落实健康第一的指导思想,切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,提高体质健康水平.某市抽调三所中学进行中学生体育达标测试,现简称为![]() 校、
校、![]() 校、
校、![]() 校.现对本次测试进行调查统计,得到测试成绩排在前200名学生层次分布的饼状图、
校.现对本次测试进行调查统计,得到测试成绩排在前200名学生层次分布的饼状图、![]() 校前200名学生的分布条形图,则下列结论不一定正确的是( )
校前200名学生的分布条形图,则下列结论不一定正确的是( )
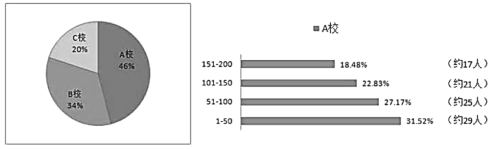
A.测试成绩前200名学生中![]() 校人数超过
校人数超过![]() 校人数的2倍
校人数的2倍
B.测试成绩前100名学生中![]() 校人数超过一半以上
校人数超过一半以上
C.测试成绩前151—200名学生中![]() 校人数最多33人
校人数最多33人
D.测试成绩前51—100名学生中![]() 校人数多于
校人数多于![]() 校人数
校人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com