
 某制药厂开发出一种新药投放市场,如果成年人按规定的剂量服用,据监测,服药后每毫升血液的含药量y(微克)与时间t(小时)之间的函数关系近似满足如图所示曲线.
某制药厂开发出一种新药投放市场,如果成年人按规定的剂量服用,据监测,服药后每毫升血液的含药量y(微克)与时间t(小时)之间的函数关系近似满足如图所示曲线.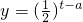 ,
,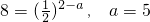 ,
,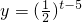 .
.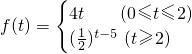 .
.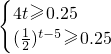 ,
, ,
,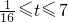 .
.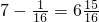 个小时.
个小时. =
=
 =
=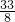 毫克.
毫克.

科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com