
分析 ①举例说明命题不成立;
②利用作差法证明命题正确;
③讨论x>0与x<0时,x+$\frac{1}{x}$的最值问题即可.
解答 解:对于①,当a<0,b<0时,$\frac{a+b}{2}≥\sqrt{ab}$不成立,∴①错误;
对于②,任意x∈R,有x2+1-x=${(x-\frac{1}{2})}^{2}$+$\frac{3}{4}$>0
∴x2+1>x,②正确;
对于③,当x>0时,x+$\frac{1}{x}$≥2,当x<0时,x+$\frac{1}{x}$≤-2;∴③错误
综上,真命题的序号是②.
故答案为:②.
点评 本题考查了不等式与不等关系的应用问题,也考查了分类讨论思想的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
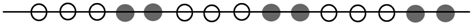
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
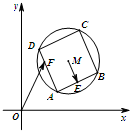 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com