
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①,“?x∈R都有x2≥0”的否定是“?x0∈R使得x02<0”;
②,当“x≠3”时“|x|=3”成立;
③,当m$>\frac{1}{2}$时,△=4-8m<0,方程mx2+2x+2=0无实数根,
解答 解:对于?①,“?x∈R都有x2≥0”的否定是“?x0∈R使得x02<0”,故错;
对于?②,当“x≠3”时“|x|=3”成立,故错;
对于?③,命题“若m≤$\frac{1}{2}$,则方程mx2+2x+2=0有实数根”的否命题为“若m>$\frac{1}{2}$,则方程mx2+2x+2=0无实数根”,∵当m$>\frac{1}{2}$时,△=4-8m<0,方程mx2+2x+2=0无实数根,故正确,
故选:B
点评 本题考查了命题真假的判定,命题的否定、否命题的区别,充要条件的判定,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
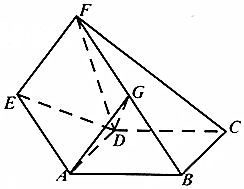 如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.
如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
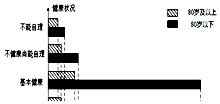 我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{π}{2})>2f(\frac{π}{6})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$ | D. | $f(1)<2f(\frac{π}{6})sin1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
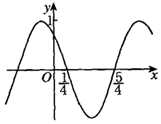 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )| A. | ω=π | |
| B. | φ=$\frac{π}{4}$ | |
| C. | f(x)的单调减区间为(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z | |
| D. | f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com