
����Ŀ��ÿ���![]() ��
��![]() ����ȫ�������գ�Ϊ��ӭ����һ���գ�ij�����������ų����˵���С�飬���顰������ʳ�뻼ȣ�ݵĹ�ϵ�����Ըõ���Сѧ���꼶
����ȫ�������գ�Ϊ��ӭ����һ���գ�ij�����������ų����˵���С�飬���顰������ʳ�뻼ȣ�ݵĹ�ϵ�����Ըõ���Сѧ���꼶![]() ��ѧ�����м�飬����ȣ�ݵIJ���ȣ�ݷ��࣬�û������ݣ���������ʳ�Ҳ���ȣ�ݵ�ѧ����
��ѧ�����м�飬����ȣ�ݵIJ���ȣ�ݷ��࣬�û������ݣ���������ʳ�Ҳ���ȣ�ݵ�ѧ����![]() ����������ʳ������ȣ�ݵ�ѧ����
����������ʳ������ȣ�ݵ�ѧ����![]() ������������ʳ�����x�ݵ�ѧ����
������������ʳ�����x�ݵ�ѧ����![]() ����
����
��1����ɴ���е�![]() ���������ʣ��ܷ��ڷ����ʲ�����
���������ʣ��ܷ��ڷ����ʲ�����![]() ��ǰ���£���Ϊ�õ���ѧ���ij�����ʳ�뻼ȣ���й�ϵ��
��ǰ���£���Ϊ�õ���ѧ���ij�����ʳ�뻼ȣ���й�ϵ��
��2��![]() �����������ŵĹ�����Ա����ֳ����飬ÿ��
�����������ŵĹ�����Ա����ֳ����飬ÿ��![]() �ˣ�һ�鸺�������ռ�����һ�鸺�����ݴ�����������Ա�ֵ������ռ������飬������Ա�ҷֵ��������ݴ�����ĸ��ʣ�
�ˣ�һ�鸺�������ռ�����һ�鸺�����ݴ�����������Ա�ֵ������ռ������飬������Ա�ҷֵ��������ݴ�����ĸ��ʣ�
����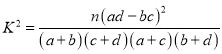
|
|
|
|
|
|
|
|
���𰸡���1�����������,���ڷ����ʲ�����0.001��ǰ���£���Ϊ�õ���ѧ���ij�����ʳ�뻼ȣ���й�ϵ��2��![]()
��������
��1������������Ϣ����![]() ���������������
���������������![]() �Ĺ۲�ֵ�������۲�ֵ��
�Ĺ۲�ֵ�������۲�ֵ��![]() ���д�С�Ƚϣ��ɶ����н��۵���������жϣ�
���д�С�Ƚϣ��ɶ����н��۵���������жϣ�
��2�������п��ܷ��������оٳ�����ȷ��ȫ���ķ���������ȷ���¼���������Ա�ֵ������ռ������飬������Ա�ҷֵ��������ݴ����顱��������������Ȼ�����ùŵ���͵ĸ��ʹ�ʽ�ɼ���������¼��ĸ���.
��1��������ɵ���������
��������ʳ | ������ʳ | �ܼ� | |
����ȣ�� |
|
|
|
��ȣ�� |
|
|
|
�ܼ� |
|
|
|
![]() ��
��
�����ڷ����ʲ�����![]() ��ǰ���£���Ϊ�õ���ѧ���ij�����ʳ�뻼ȣ���й�ϵ��
��ǰ���£���Ϊ�õ���ѧ���ij�����ʳ�뻼ȣ���й�ϵ��
��2��������������ԱΪ���Ͷ���
�� |
|
|
|
|
|
|
�ռ����� | ���� | �ױ� | �� | �ұ� | �Ҷ� | ���� |
�������� | ���� | �Ҷ� | �ұ� | �� | �ױ� | ���� |
���������ܹ���![]() �֣�
�֣�
������Ա�����ռ������ҹ�����Ա�Ҹ���������ռ![]() �飬�ֱ��ǵ�
�飬�ֱ��ǵ�![]() ��͵�
��͵�![]() ��.
��.
���Թ�����Ա�ֵ������ռ������飬������Ա�ҷֵ��������ݴ�����ĸ���![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��
�У���֪��![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �������ǵ�б��֮����
�������ǵ�б��֮����![]() ���ǵ�
���ǵ�![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() ��
��
������![]() �ķ��̣�
�ķ��̣�
������ֱ֪��![]() ��
��![]() �ֱ�ֱ��
�ֱ�ֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() ���켣
���켣![]() �ڵ�
�ڵ�![]() �����������߶�
�����������߶�![]() ���ڵ�
���ڵ�![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �У�
�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
�� ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() .��
.��![]() ��
��![]() ����
����![]() ��λ�ã�ʹ��ƽ��
��λ�ã�ʹ��ƽ��![]() ƽ��
ƽ��![]() ����ͼ2.
����ͼ2.
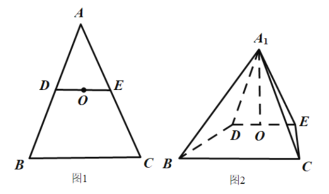
��1����֤��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �������ǵ�б��֮��Ϊ
�������ǵ�б��֮��Ϊ![]() ���Ƕ���
���Ƕ���![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ��
��
��1��������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��������
��ֱ��������![]() ����
����![]() ��
��![]() ���㣬�Ƿ���ڶ���
���㣬�Ƿ���ڶ���![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��
��![]() б��֮��Ϊ��ֵ�������ڣ����
б��֮��Ϊ��ֵ�������ڣ����![]() ���ꣻ�������ڣ���˵�����ɡ�
���ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() �����Ҷ���ֱ�Ϊ
�����Ҷ���ֱ�Ϊ![]() ��
��![]() ���϶���ΪB���ҽ���ΪF����ֱ֪��
���϶���ΪB���ҽ���ΪF����ֱ֪��![]() ����б��Ϊ120����
����б��Ϊ120����![]() .
.
(1)����ԲC�ķ��̣�
(2)��PΪ��ԲC�ϲ�ͬ��![]() ��
��![]() ��һ�㣬OΪ����ԭ�㣬�߶�
��һ�㣬OΪ����ԭ�㣬�߶�![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ��M�㣬��M�Ҵ�ֱ��
��M�㣬��M�Ҵ�ֱ��![]() ��ֱ�߽�y����Q�㣬��
��ֱ�߽�y����Q�㣬��![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��Բ�ķ���Ϊ��
�У���֪��Բ�ķ���Ϊ��![]() ������
������![]() ����Բ�ϣ�
����Բ�ϣ�![]() Ϊԭ�㣬�߶�
Ϊԭ�㣬�߶�![]() ���е�Ϊ
���е�Ϊ![]() .
.
��1����![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���ᣬ����������ϵ�����
���������Ϊ���ᣬ����������ϵ�����![]() �Ĺ켣�ļ����귽�̣�
�Ĺ켣�ļ����귽�̣�
��2����ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ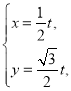 ��
��![]() ��������
��������![]() ���
���![]() �Ĺ켣����
�Ĺ켣����![]() ��
��![]() ���㣬���ҳ�
���㣬���ҳ�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��1����![]() ���ı���
���ı���![]() �������
�������
��2����E��BD���е㣬��CE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����D��ABC���ĸ���������O�������ϣ���AB��AC��BC��DB��DC��1��������D��ABC�����ȡ�����ֵʱ����O�ı����Ϊ(������)
A. ![]() B. 2��C. 5��D.
B. 2��C. 5��D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A����2��1����B��2��4������P��ֱ��l��y��x�ϵĶ���.
��1����PA��PB�����P�����ꣻ
��2�����A��ֱ��l1���B��ֱ��l2��ƽ����l����l1��l2֮��ľ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com