
分析 利用线面的关系,结合图形逐步判断:①中线面关系,由若n⊥β,m∥n,知m⊥β,则m∥α或m?α;
②面面平行的判定定理:一个平面内两条交线和另一平面平行,则这两平面平行;
③线线位置关系考查:相交,平行和异面,由题知不平行;
④线面垂直的判定定理.
解答 解:①若n⊥β,m∥n,n?α,则m∥α或m?α,故A错误;
②若m?α,n?α,m∥β,n∥β,且m,n相交,则α∥β,故B错误;
③若α∥β,m?α,n?β,则m,n没有交点,所以平行或异面,故C错误;
④若α⊥β,α∩β=m,n?α,n⊥m,则n⊥β,故D正确.
故答案为④.
点评 考查了线面,线线的位置关系,应紧扣定理,性质,不能随意猜测.


科目:高中数学 来源: 题型:填空题
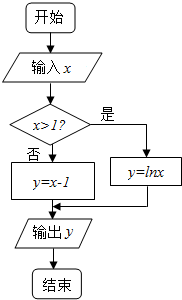 某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.
某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-3) | B. | f(3)>f(2) | C. | f(-2)>f(3) | D. | f(2)>f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com