
分析 (1)根据二次函数的性质求出ac=4,根据基本不等式的性质求出$\frac{1}{c}$+$\frac{9}{a}$的最小值即可;(2)问题转化为-1,2是方程ax2-4x+c=0的解,求出a,c的值即可.
解答 解:∵二次函数f(x)=ax2-4x+c的值域为[0,+∞),
∴$\left\{\begin{array}{l}{a>0}\\{△=16-4ac=0}\end{array}\right.$,
解得a>0,c>0,ac=4,
∴$\frac{1}{c}$+$\frac{9}{a}$≥2$\sqrt{\frac{9}{ac}}$=2$\sqrt{\frac{9}{4}}$=3,
若ax2-4x+c>0的解集为 (-1,2),
则-1,2是方程ax2-4x+c=0的解,
∴$\left\{\begin{array}{l}{a+4+c=0}\\{4a-8+c=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=4}\\{c=-8}\end{array}\right.$,
∴a-c=12,
故答案为:3,12.
点评 本题考查了二次函数的性质,考查基本不等式的性质,是一道基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
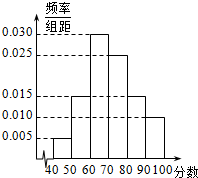 某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.
某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份x | 1 | 2 | 3 | 4 | 5 |
| 收入y(千元) | 21 | 24 | 27 | 29 | 31 |
| 受培时间一年以上 | 受培时间不足一年 | ||
| 收入不低于平均值 | 60 | 20 | |
| 收入低于平均值 | 10 | 10 | |
| 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
| k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (0,2) | C. | (-1,0) | D. | (2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com