
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,设函数
时,设函数![]() ,若存在区间
,若存在区间![]() ,使得函数
,使得函数![]() 在
在![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() (2)答案不唯一,见解析 (3)
(2)答案不唯一,见解析 (3)![]()
【解析】
(1)求导,接着单调区间,即可得出最小值;
(2)求导,对![]() 分类讨论,可求出函数
分类讨论,可求出函数![]() 的单调区间;
的单调区间;
(3)求出![]() ,通过分析
,通过分析![]() ,可得到
,可得到![]() 在
在![]() 增函数,从而有
增函数,从而有![]() ,转化为
,转化为![]() 在
在![]() 上至少有两个不同的正根
上至少有两个不同的正根![]() ,
,![]() ,转化为
,转化为![]() 与
与![]()
![]() 至少有两个交点,即可求出实数
至少有两个交点,即可求出实数![]() 的最大值.
的最大值.
(1)当![]() 时,
时,![]() ,
,
这时的导数![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() 得到
得到![]() ,
,
令![]() 得到
得到![]() ,
,
故函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
故函数![]() 在
在![]() 时取到最小值,
时取到最小值,
故![]() ;
;
(2)当![]() 时,函数
时,函数![]()
导数为![]() ,
,
若![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
若![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
即函数![]() 在区间
在区间![]() ,
,![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增.
上单调递增.
若![]() 时,
时,![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
函数![]() 在区间
在区间![]() ,
,![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增.
上单调递增.
综上,若![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,无增区间,
,无增区间,
若![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,
,![]() ,增区间为
,增区间为![]() ,
,
若![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,
,![]() ,增区间为
,增区间为![]() .
.
(3)当![]() 时,设函数
时,设函数![]() .
.
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
![]() ,
,![]() 为增函数,
为增函数,
![]() 在区间
在区间![]() 上递增,
上递增,
∵![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
所以![]() 在
在![]() 上至少有两个不同
上至少有两个不同
的正根![]() ,
,![]() ,
,
令![]() ,求导得,
,求导得,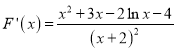 ,
,
令![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 递增,
递增,![]() ,
,![]() ,
,
当![]() ,
,![]() ,∴
,∴![]() ,
,
当![]() ,
,![]() ,∴
,∴![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() ,∴
,∴![]() ,
,
∴![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,食甚时刻为21时31分,22时08分生光,直至23时12分复圆.全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”将在食甚时刻开始,生光时刻结東,一市民准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设S、T是R的两个非空子集,如果函数![]() 满足:①
满足:①![]() ;②对任意
;②对任意![]() ,
,![]() ,当
,当![]() 时,恒有
时,恒有![]() ,那么称函数
,那么称函数![]() 为集合S到集合T的“保序同构函数”.
为集合S到集合T的“保序同构函数”.
(1)试写出集合![]() 到集合R的一个“保序同构函数”;
到集合R的一个“保序同构函数”;
(2)求证:不存在从集合Z到集合Q的“保序同构函数”;
(3)已知![]() 是集合
是集合![]() 到集合
到集合![]() 的“保序同构函数”,求s和t的最大值.
的“保序同构函数”,求s和t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国足球超级联赛某一季的收官阶段中,广州恒大淘宝、北京中赫国安、上海上港、山东鲁能泰山分别积分59分、58分、56分、50分,四家俱乐部都有机会夺冠.A,B,C三个球迷依据四支球队之前比赛中的表现,结合自已的判断,对本次联赛的冠军进行如下猜测:![]() 猜测冠军是北京中赫国安或山东鲁能泰山;
猜测冠军是北京中赫国安或山东鲁能泰山;![]() 猜测冠军一定不是上海上港和山东鲁能泰山;
猜测冠军一定不是上海上港和山东鲁能泰山;![]() 猜测冠军是广州恒大淘宝或北京中赫国安.联赛结束后,发现A,B,C三人中只有一人的猜测是正确的,则冠军是( )
猜测冠军是广州恒大淘宝或北京中赫国安.联赛结束后,发现A,B,C三人中只有一人的猜测是正确的,则冠军是( )
A.广州恒大淘宝B.北京中赫国安C.上海上港D.山东鲁能泰山
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,圆
为坐标原点,圆![]() ,定点
,定点![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 的半径
的半径![]() 于点
于点![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() 是曲线
是曲线![]() 上但不在坐标轴上的任意一点,曲线
上但不在坐标轴上的任意一点,曲线![]() 与
与![]() 轴的焦点分别为
轴的焦点分别为![]() ,直线
,直线![]() 和
和![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,请问线段长之积
两点,请问线段长之积![]() 是否为定值?如果还请求出定值,如果不是请说明理由;
是否为定值?如果还请求出定值,如果不是请说明理由;
(3)在(2)的条件下,若点![]() 坐标为(-1,0),设过点
坐标为(-1,0),设过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的2个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲,乙两个盒内各取2个球.
(1)求取出的4个球中恰有1个红球的概率;
(2)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
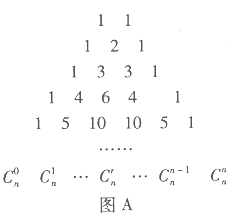
【题目】在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图![]() 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”
所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”![]() ,如图
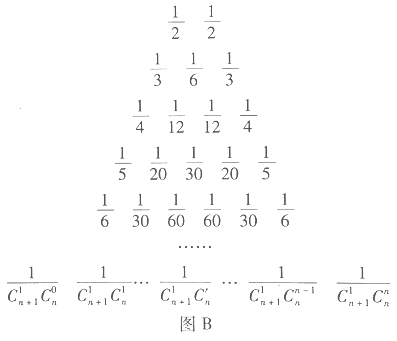
,如图![]() .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图
.17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图![]() .在杨辉三角中,相邻两行满足关系式:
.在杨辉三角中,相邻两行满足关系式:![]() ,其 中
,其 中![]() 是行数,
是行数,![]() .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
.请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com