
【题目】某公司采用招考方式引进人才,规定必须在![]() 、
、![]() 、
、![]() 三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每个测试点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每个测试点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 、
、![]() 、
、![]() 测试合格的概率分别为
测试合格的概率分别为![]() 、
、![]() 、
、![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 、
、![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 、
、![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)![]() 、
、![]() 测试点,理由见解析;(2)分布列见解析,
测试点,理由见解析;(2)分布列见解析,![]() .
.
【解析】
(1)利用独立事件的概率乘法公式分别计算出小李选择![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]() 测试点测试合格的概率,比较大小后可得出结论;
测试点测试合格的概率,比较大小后可得出结论;
(2)由题意可知,随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,利用独立事件的概率乘法公式计算出随机变量
,利用独立事件的概率乘法公式计算出随机变量![]() 在不同取值下的概率,可得出随机变量
在不同取值下的概率,可得出随机变量![]() 的概率分布列,进而可求得随机变量
的概率分布列,进而可求得随机变量![]() 的数学期望
的数学期望![]() 的值.
的值.
(1)设考生小李在![]() 、
、![]() 、
、![]() 各测试点测试合格记为事件
各测试点测试合格记为事件![]() 、
、![]() 、
、![]() ,且各个事件相互独立,由题意
,且各个事件相互独立,由题意![]() ,
,![]() ,
,![]() ,
,
若选择在![]() 、
、![]() 测试点测试,则参加面试的概率为
测试点测试,则参加面试的概率为![]() ;
;
若选择在![]() 、
、![]() 测试点测试,则参加面试的概率为
测试点测试,则参加面试的概率为![]() ;
;
若选择在![]() 、
、![]() 测试点测试,则参加面试的概率为
测试点测试,则参加面试的概率为![]() .
.
因为![]() ,所以小李选择在
,所以小李选择在![]() 、
、![]() 测试点测试参加面试的可能性最大;
测试点测试参加面试的可能性最大;
(2)记小李在![]() 、
、![]() 测试点测试合格记为事件
测试点测试合格记为事件![]() 、
、![]() ,记小王在
,记小王在![]() 、
、![]() 测试点测试合格记为事件
测试点测试合格记为事件![]() 、
、![]() ,则
,则![]() ,
,![]() ,且
,且![]() 的所有可能取值为
的所有可能取值为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
所以![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.
所以随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】(1)已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.
(2)有一个正四棱台形状的油槽,可以装油190L,假如它的两底面长分别等于60cm和40cm,求它的深度为多少cm?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.

(1)求出第4组的频率,并补全频率分布直方图;
(2)根据样本频率分布直方图估计样本的中位数与平均数;
(3)如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
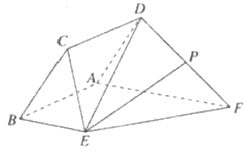
【题目】如图,已知菱形![]() 与直角梯形
与直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜欢数学是否与性别有关,对本班![]() 人进行了问卷调查得到了如下的列联表,已知在全部
人进行了问卷调查得到了如下的列联表,已知在全部![]() 人中随机抽取
人中随机抽取![]() 人抽到喜欢数学的学生的概率为
人抽到喜欢数学的学生的概率为![]() .
.
喜欢数学 | 不喜欢数学 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过![]() 的前提下认为喜欢数学与性别有关?说明你的理由;
的前提下认为喜欢数学与性别有关?说明你的理由;
(3)现从女生中抽取![]() 人进一步调查,设其中喜欢数学的女生人数为
人进一步调查,设其中喜欢数学的女生人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
下面的临界表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.

(1)求![]() 的值;
的值;
(2)分别求出甲、乙两组数据的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从A,B、C,D,E五人中选取三人参加一个重要会议,五人中每个人被选中的机会均相等,求:
(1)A和B都被选中的概率;
(2)A和B至少有一个被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于方程为![]() 的曲线
的曲线![]() 给出以下三个命题:
给出以下三个命题:
(1)曲线![]() 关于原点对称;(2)曲线
关于原点对称;(2)曲线![]() 关于
关于![]() 轴对称,也关于
轴对称,也关于![]() 轴对称,且
轴对称,且![]() 轴和
轴和![]() 轴是曲线
轴是曲线![]() 仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点
仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点![]() ,都在曲线
,都在曲线![]() 上,则四边形
上,则四边形![]() 每一条边的边长都大于2;
每一条边的边长都大于2;
其中正确的命题是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球,两个“
”号球,两个“![]() ”号球,三个“
”号球,三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球,五个“
”号球,五个“![]() ”号球,每次摸奖后放回,每位顾客消费额满
”号球,每次摸奖后放回,每位顾客消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金。
元,摸得无号球则没有奖金。
(1)经统计,顾客消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 位顾客,请估计消费额
位顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数.(结果四舍五入取整数)
内并中奖的人数.(结果四舍五入取整数)
附:若![]() ,则
,则![]() ,
,![]() .
.
(2)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列.
的分布列.
(3)某顾客消费额为![]() 元,有两种摸奖方法,
元,有两种摸奖方法,
方法一:三次![]() 箱内摸奖机会;
箱内摸奖机会;
方法二:一次![]() 箱内摸奖机会.
箱内摸奖机会.
请问:这位顾客选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com