
【题目】(1)已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.
(2)有一个正四棱台形状的油槽,可以装油190L,假如它的两底面长分别等于60cm和40cm,求它的深度为多少cm?
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
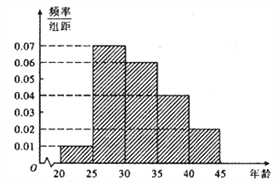
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,点
的中点,点![]() 为上底面的中心,过
为上底面的中心,过![]() ,
,![]() ,
,![]() 三点的平面把正方体分为两部分,其中含
三点的平面把正方体分为两部分,其中含![]() 的部分为
的部分为![]() ,不含
,不含![]() 的部分为
的部分为![]() ,连结
,连结![]() 和
和![]() 的任一点
的任一点![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() 的最大值为
的最大值为

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 在线段
在线段![]() 上,且
上,且![]() ,过
,过![]() 、
、![]() 、
、![]() 三点的平面将多面体
三点的平面将多面体![]() 分成两部分,设上、下两部分的体积分别为
分成两部分,设上、下两部分的体积分别为![]() 、
、![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD.
(1)求证:EF∥平面PAD;
(2)若EF⊥PC,求证:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过两点
经过两点![]() ,
,![]() ,且圆心
,且圆心![]() 在直线
在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,点
两点,点![]() 为圆
为圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 交
交![]() 轴于
轴于![]() 、
、![]() 点.当点
点.当点![]() 变化时,以
变化时,以![]() 为直径的圆
为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论.
内一定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有正整数构成的数表如下:
第一行:1
第二行:12
第三行:1123
第四行:11211234
第五行:1121123112112345
…
第k行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,…,直至按原序抄写第k﹣1行,最后添上数k.(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).将按照上述方式写下的第n个数记作![]() (如
(如![]() ,…),用
,…),用![]() 表示数表第
表示数表第![]() 行的数的个数,求数列{
行的数的个数,求数列{![]() }的前
}的前![]() 项和
项和![]() =____
=____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司采用招考方式引进人才,规定必须在![]() 、
、![]() 、
、![]() 三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每个测试点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每个测试点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 、
、![]() 、
、![]() 测试合格的概率分别为
测试合格的概率分别为![]() 、
、![]() 、
、![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 、
、![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 、
、![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com