
【题目】现有正整数构成的数表如下:
第一行:1
第二行:12
第三行:1123
第四行:11211234
第五行:1121123112112345
…
第k行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,…,直至按原序抄写第k﹣1行,最后添上数k.(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).将按照上述方式写下的第n个数记作![]() (如
(如![]() ,…),用
,…),用![]() 表示数表第
表示数表第![]() 行的数的个数,求数列{
行的数的个数,求数列{![]() }的前
}的前![]() 项和
项和![]() =____
=____
科目:高中数学 来源: 题型:
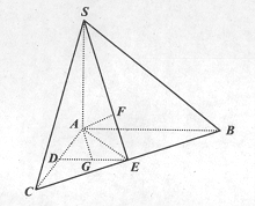
【题目】如图,在三棱锥S-ABC中,SA ⊥底面ABC,AC=AB=SA=2,AC ⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE.
(Ⅰ)求异面直线AF与DE所成角的余弦值;
(Ⅱ)求证:AF⊥平面SBC;
(Ⅲ)设G为线段DE的中点,求直线AG与平面SBC所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.
(2)有一个正四棱台形状的油槽,可以装油190L,假如它的两底面长分别等于60cm和40cm,求它的深度为多少cm?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,离心率
,离心率![]() ,且短轴长为4.
,且短轴长为4.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 已知
已知![]() ,
,![]() ,若直线l与圆
,若直线l与圆![]() 相切,且交椭圆E于C、D两点,记
相切,且交椭圆E于C、D两点,记![]() 的面积为
的面积为![]() ,记
,记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.

(1)求出第4组的频率,并补全频率分布直方图;
(2)根据样本频率分布直方图估计样本的中位数与平均数;
(3)如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
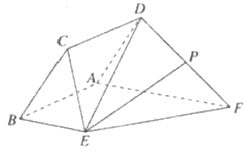
【题目】如图,已知菱形![]() 与直角梯形
与直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于方程为![]() 的曲线
的曲线![]() 给出以下三个命题:
给出以下三个命题:
(1)曲线![]() 关于原点对称;(2)曲线
关于原点对称;(2)曲线![]() 关于
关于![]() 轴对称,也关于
轴对称,也关于![]() 轴对称,且
轴对称,且![]() 轴和
轴和![]() 轴是曲线
轴是曲线![]() 仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点
仅有的两条对称轴;(3)若分别在第一、第二、第三、第四象限的点![]() ,都在曲线
,都在曲线![]() 上,则四边形
上,则四边形![]() 每一条边的边长都大于2;
每一条边的边长都大于2;
其中正确的命题是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com