
分析 (Ⅰ)分别求导,根据导数和函数的单调性,求出函数的单调性区间,再根据f(x)和F(x)在区间(0,ln3)内具有相同的单调性,即可求出a的范围,
(Ⅱ)先求导,再令其导数为0,得到a=$\frac{1-lnx}{{x}^{2}}$,再构造函数p(x)=$\frac{1-lnx}{{x}^{2}}$,利用导数求出p(x)的最小值,即可得到函数g(x)的单调区间,求出g(x)的最小值,
再构造函数,求出最值即可.
解答 解:(Ⅰ)求导,$f'(x)=a-\frac{1}{x}=\frac{ax-1}{x}$,F'(x)=ex+x,x>0,a<0,
f'(x)<0在(0,+∞)上恒成立,即f(x)在(0,+∞)上单调递减,
当-1≤a<0时,F'(x)>0,即F(x)在(0,+∞)上单调递增,不合题意
当a<-1时,由F'(x)>0,得x>ln(-a),由F'(x)<0,得0<x<ln(-a),
∴F(x)的单调减区间为(0,ln(-a)),单调增区间为(ln(-a),+∞)
∵f(x)和F(x)在区间(0,ln3)上具有相同的单调性,
∴ln(-a)≥ln3,解得:a≤-3,
综上,a的取值范围是(-∞,-3];
(Ⅱ)$g'(x)={e^{ax-1}}+ax{e^{ax-1}}-a-\frac{1}{x}=({ax+1})({{e^{ax-1}}-\frac{1}{x}})$,
由${e^{ax-1}}-\frac{1}{x}=0$,解得:$a=\frac{1-lnx}{x}$,
设$p(x)=\frac{1-lnx}{x}$,则$p'(x)=\frac{lnx-2}{x^2}$,
当x>e2时,p'(x)>0,当0<x<e2,p'(x)<0,
从而p(x)在(0,e2)上单调递减,在(e2,+∞)上单调递增,
$p{(x)_{min}}=p({e^2})=-\frac{1}{e^2}$,
当$a≤-\frac{1}{e^2},a≤\frac{1-lnx}{x}$,即${e^{ax-1}}-\frac{1}{x}≤0$,
在$({0,-\frac{1}{a}})$上,ax+1>0,g'(x)≤0,g(x)单调递增,
在$({\frac{1}{a},+∞})$上,ax+1<0,g'(x)≥0,g(x)单调递增,
∴$g{(x)_{min}}=g({-\frac{1}{a}})=M$,
设$t=-\frac{1}{a}$∈(0,e2],
$M=h(t)=\frac{t}{e^2}-lnt+1,({0<t≤{e^2}})$,
∴$h'(t)=\frac{1}{e^2}-\frac{1}{t}≤0$,h(x)在∈(0,e2]上单调递减,
∴h(t)≥h(e2)=0,
∴M的最小值为0.
点评 本题考查了导数研究函数的极值,考查分类整合思想、转化思想,考查学生综合运用知识分析解决问题的能力,属于难题


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
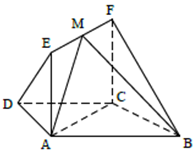 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com