
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
【答案】![]() Ⅰ
Ⅰ![]() 详见解析;
详见解析;![]() Ⅱ
Ⅱ![]() ①
①![]() ,②
,②![]() 或
或![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 可以通过已知证明出
可以通过已知证明出![]() 平面PAB,这样就可以证明出
平面PAB,这样就可以证明出![]() ;
;
![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,可以求出相应点的坐标,求出平面PBC的法向量为![]() 、平面PCD的法向量
、平面PCD的法向量![]() ,利用空间向量的数量积,求出二面角
,利用空间向量的数量积,求出二面角![]() 的大小;
的大小;
![]() 求出平面PBC的法向量,利用线面角的公式求出
求出平面PBC的法向量,利用线面角的公式求出![]() 的值.
的值.
证明:![]() Ⅰ
Ⅰ![]() 在图1中,
在图1中,![]() ,
,![]() ,
,

![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() ,
,![]() ,
,
当![]() 沿AD折起时,
沿AD折起时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 平面PAB,
平面PAB,
又![]() 平面PAB,
平面PAB,![]() .
.
解:![]() Ⅱ
Ⅱ![]() 以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于
以点A为坐标原点,分别以AB,AD,AP为x,y,z轴,建立空间直角坐标系,由于![]() 平面ABCD
平面ABCD
则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]()
![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
设平面PBC的法向量为![]() y,
y,![]() ,
,
则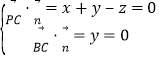 ,取
,取![]() ,得
,得![]() 0,
0,![]() ,
,
设平面PCD的法向量![]() b,
b,![]() ,
,
则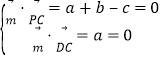 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,可知为钝角,
,可知为钝角,
则![]() ,
,![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
![]() 设AM与面PBC所成角为
设AM与面PBC所成角为![]() ,
,
![]() 0,
0,![]() ,1,
,1,![]() ,
,![]() ,
,![]() ,
,
平面PBC的法向量![]() 0,
0,![]() ,
,
![]() 直线AM与平面PBC所成的角为
直线AM与平面PBC所成的角为![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2 ![]() .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC. 
(1)证明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
(1)求样本容量n和频率分布直方图中x、y的值;
(2)根据样本直方图估计所取样本的中位数及平均数(同一组数据用该区间的中点值作代表).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】位于潍坊滨海的“滨海之眼”摩天轮是世界上最高的无轴摩天轮,该摩天轮的直径均为124米,中间没有任何支撑,摩天轮顺时针匀速旋转一圈需要30分钟,当乘客乘坐摩天轮到达最高点时,距离地面145米,可以俯瞰白浪河全景,图中![]() 与地面垂直,垂足为点
与地面垂直,垂足为点![]() ,某乘客从
,某乘客从![]() 处进入
处进入![]() 处的观景舱,顺时针转动
处的观景舱,顺时针转动![]() 分钟后,第1次到达
分钟后,第1次到达![]() 点,此时
点,此时![]() 点与地面的距离为114米,则
点与地面的距离为114米,则![]() ( )
( )

A. 16分钟B. 18分钟C. 20分钟D. 22分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入a(单位:万元)满足![]() ,乙城市收益Q与投入a(单位:万元)满足
,乙城市收益Q与投入a(单位:万元)满足![]() ,设甲城市的投入为x(单位:万元),两个城市的总收益为
,设甲城市的投入为x(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)求![]() 及定义域;
及定义域;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实常数,y=f(x)是定义在R上的奇函数,当x<0时,f(x)=9x+ ![]() +7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
+7.若f(x)≥a+1对一切x≥0成立,则a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过![]() 小时的
小时的![]() 名大学生,将
名大学生,将![]() 人使用手机的时间分成
人使用手机的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 |
|
|
|
|
|

(1)完成频率分布直方图;
(2)根据频率分布直方图估计大学生使用手机的平均时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C1: ![]() 的焦点与双曲线C2:
的焦点与双曲线C2: ![]() 的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( )
的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com