
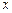 轴相切,圆心在直线
轴相切,圆心在直线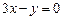 上,且被直线
上,且被直线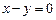 截下的弦长为
截下的弦长为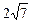 的圆的方程。
的圆的方程。 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源:不详 题型:单选题
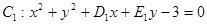 和
和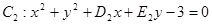 都过点E(3,4),则经过两点
都过点E(3,4),则经过两点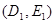 、
、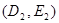 的直线方程为
的直线方程为| A.3x+4y+22=0 | B.3x-4y+22="0" | C.4x+3y+22=0 | D.4x-3y-22="0" |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,动点
中,动点 到两圆
到两圆 的圆心
的圆心 和
和 的距离的和等于
的距离的和等于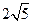 .
. 的轨迹方程;
的轨迹方程; 的轨迹与
的轨迹与 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com