
分析 由双曲线的标准方程,求得焦点坐标,求得p的值,设A点坐标,根据向量的坐标运算求得$\overrightarrow{OM}$=($\frac{{y}_{0}^{2}}{12}$+$\frac{2}{3}$,$\frac{{y}_{0}}{3}$),利用直线的斜率公式及基本不等式的性质,即可求得直线OM斜率的最大值.
解答 解:由双曲线的标准方程:$\frac{{x}^{2}}{\frac{1}{2}}-\frac{{y}^{2}}{\frac{1}{2}}=1$,则a2=$\frac{1}{2}$,b2=$\frac{1}{2}$,
则c2=a2+b2=1,则双曲线的焦点F(±1,0),p=2,
则抛物线y2=4x的焦点(1,0),设A($\frac{{y}_{0}^{2}}{4}$,y0),
显然当y0<0,kOM<0;当y0>0,kOM>0.
要求kOM的最大值,设y0>0,
则$\overrightarrow{OM}$=$\overrightarrow{OF}$+$\overrightarrow{FM}$=$\overrightarrow{OF}$+$\frac{1}{3}$$\overrightarrow{FA}$=$\overrightarrow{OF}$+$\frac{1}{3}$($\overrightarrow{OA}$-$\overrightarrow{OF}$)
=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OF}$=($\frac{{y}_{0}^{2}}{12}$+$\frac{2}{3}$,$\frac{{y}_{0}}{3}$),
可得kOM=$\frac{\frac{{y}_{0}}{3}}{\frac{{y}_{0}^{2}}{12}+\frac{2}{3}}$=$\frac{2}{\frac{{y}_{0}}{2}+\frac{4}{{y}_{0}}}$≤$\frac{2}{2\sqrt{\frac{{y}_{0}}{2}×\frac{4}{{y}_{0}}}}$=$\frac{\sqrt{2}}{2}$,
当且仅当y02=8,即y0=2$\sqrt{2}$,取得等号.
直线OM斜率的最大值$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查双曲线的简单几何性质,向量数量积的坐标运算,直线的斜率公式,考查计算能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
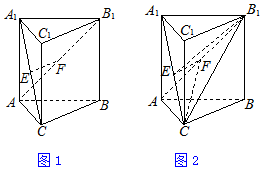 如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
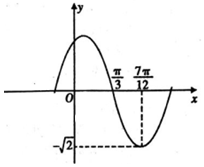 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | B. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
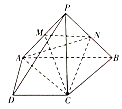 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com