
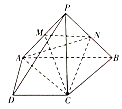
 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥分析 (1)由题意可得AC⊥PC,由AC2+BC2=AB2,可求得AC⊥BC,从而有AC⊥平面PBC,利用面面垂直的判定定理即可证得平面PAC⊥平面PBC;
(2)在三棱锥P-ABC中利用等积法求得C到平面PAB的距离,再求出三角形AMN的面积,进一步由等积法求得三棱锥A-CMN的体积.
解答 (1)证明:∵PC⊥平面ABCD,AC?平面ABCD,
∴AC⊥PC,
∵AB=4,AD=CD=2,
∴AC=BC=$2\sqrt{2}$,
∴AC2+BC2=AB2,
∴AC⊥BC,
又BC∩PC=C,
∴AC⊥平面PBC,
∵AC?平面PAC,
∴平面PBC⊥平面PAC;
(2)解:由PC⊥CA,PC⊥CB,且PC=2,AC=BC=$2\sqrt{2}$,可得PA=PB=2$\sqrt{3}$,
又AB=4,∴${S}_{△PAB}=\frac{1}{2}×4×\sqrt{(2\sqrt{3})^{2}-{2}^{2}}=4\sqrt{2}$.
设C到平面PAB的距离为h,由等积法可得:$\frac{1}{3}×4\sqrt{2}h=\frac{1}{3}×\frac{1}{2}×$$2\sqrt{2}×2\sqrt{2}×2$,得h=$\sqrt{2}$.
${S}_{△AMN}=\frac{1}{4}{S}_{△PAB}=\frac{1}{4}$×$4\sqrt{2}=\sqrt{2}$.
∴${V}_{A-CMN}={V}_{C-AMN}=\frac{1}{3}×\sqrt{2}×\sqrt{2}=\frac{2}{3}$.
点评 本题考查平面与平面垂直的判定,考查点、线、面间的距离计算,突出几何体体积轮换公式的考查与应用,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 抛物线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.
已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
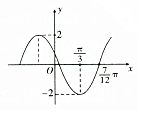 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=1,则cos(2α+$\frac{π}{3}$)的值是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=1,则cos(2α+$\frac{π}{3}$)的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{17}}}{6}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com