
分析 (I)f′(x)=3x2+2ax+b,由于函数f(x)=x3+ax2+bx(x>0)的图象与x轴相切于点(3,0).可得f′(3)=27+6a+b=0,f(3)=27+9a+3b=0,联立解得a,b.即可得出.
(II)命题p:?x1,x2∈[-1,1],|g(x1)-g(x2)|>1为假命题,等价于:命题:?x1,x2∈[-1,1],|g(x1)-g(x2)|≤1为真命题.由g(x)+f(x)=-6x2+(3c+9)x,可得g(x)=-x3+3cx.由命题:?x1,x2∈[-1,1],|g(x1)-g(x2)|≤1为真命题,可得|g(1)-g(-1)|≤1,解得c范围.又g′(x)=-3x2+3c=-3$(x+\sqrt{c})$$(x-\sqrt{c})$.利用单调性与奇偶性,只需|g($\sqrt{c}$)-g(-$\sqrt{c}$)|≤1,解得c,进而得出c的取值范围.
(III)h(x)+f(x)=x3-7x2+9x+clnx(c是与x无关的负数),h(x)=clnx-x2,(x>0).h′(x)=$\frac{c}{x}$-2x<0,因此函数h(x)在(0,+∞)上单调递减,h(x)至多有一个零点.再利用函数零点判定定理即可判断出是否有零点.
解答 解:(I)f′(x)=3x2+2ax+b,∵函数f(x)=x3+ax2+bx(x>0)的图象与x轴相切于点(3,0).
∴f′(3)=27+6a+b=0,f(3)=27+9a+3b=0,联立解得:a=-6,b=9.
∴f(x)=x3-6x2+9x.
(II)命题p:?x1,x2∈[-1,1],|g(x1)-g(x2)|>1为假命题,等价于:命题:?x1,x2∈[-1,1],|g(x1)-g(x2)|≤1为真命题.∵g(x)+f(x)=-6x2+(3c+9)x,∴g(x)=-x3+3cx.
由命题:?x1,x2∈[-1,1],|g(x1)-g(x2)|≤1为真命题,可得|g(1)-g(-1)|≤1,解得:$\frac{1}{6}≤c≤\frac{1}{2}$.
又g′(x)=-3x2+3c=-3$(x+\sqrt{c})$$(x-\sqrt{c})$.可得:函数g(x)在$[-1,-\sqrt{c})$,$(\sqrt{c},1]$内为减函数,在$[-\sqrt{c},\sqrt{c}]$内为增函数.
∵函数g(x)为奇函数,且|g(1)-g(-1)|≤1,∴只需|g($\sqrt{c}$)-g(-$\sqrt{c}$)|≤1,则:4c$\sqrt{c}$≤1,解得c≤$\frac{\root{3}{4}}{4}$.
综上可得:c的取值范围是$\frac{1}{6}$≤c≤$\frac{\root{3}{4}}{4}$.
(III)h(x)+f(x)=x3-7x2+9x+clnx(c是与x无关的负数),∴h(x)=clnx-x2,(x>0).
h′(x)=$\frac{c}{x}$-2x<0,因此函数h(x)在(0,+∞)上单调递减,h(x)至多有一个零点.
∵c<0,∴(c-1)2>1,0<${e}^{\frac{(c-1)^{2}}{c}}$<1,∴$h({e}^{\frac{(c-1)^{2}}{c}})$=(c-1)2-${e}^{\frac{(c-1)^{2}}{c}}$•${e}^{\frac{(c-1)^{2}}{c}}$>0,h(1)=-1<0.
∴函数h(x)在$({e}^{\frac{(c-1)^{2}}{c}},1)$内有一个零点,因此函数h(x)在(0,+∞)上恰有一个零点.
点评 本题考查了利用对数研究函数的单调性极值与最值与切线方程、等价转化问题、函数零点问题,考查了楼梯那里与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
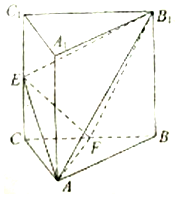 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
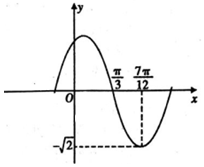 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | B. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
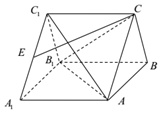 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E为A1C1的中点,$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E为A1C1的中点,$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
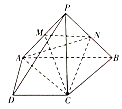 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com