
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{17}}}{6}$ | D. | $\frac{5}{3}$ |
分析 以AC的中点为原点,以ACx轴,建立如图所示的平面直角坐标系,设P的坐标为($\frac{5}{2}$cosθ,$\frac{5}{2}$sinθ),求出点B的坐标,根据向量的坐标和向量的数乘运算得到x+y=$\frac{5}{6}$sin(θ+φ)+$\frac{1}{2}$,根据正弦函数的图象和性质即可求出答案
解答 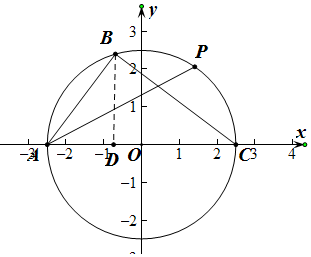 解:以AC的中点为原点,以ACx轴,建立如图所示的平面直角坐标系,
解:以AC的中点为原点,以ACx轴,建立如图所示的平面直角坐标系,
则△ABC外接圆的方程为x2+y2=2.52,
设P的坐标为($\frac{5}{2}$cosθ,$\frac{5}{2}$sinθ),
过点B作BD垂直x轴,
∵sinA=$\frac{4}{5}$,AB=3
∴BD=ABsinA=$\frac{12}{5}$,AD=AB•cosA=$\frac{3}{5}$×3=$\frac{9}{5}$,
∴OD=AO-AD=2.5-$\frac{9}{5}$=$\frac{7}{10}$,
∴B(-$\frac{7}{10}$,$\frac{12}{5}$),
∵A(-$\frac{5}{2}$,0),C($\frac{5}{2}$,0)
∴$\overrightarrow{AB}$=($\frac{9}{5}$,$\frac{12}{5}$),$\overrightarrow{AC}$=(5,0),$\overrightarrow{AP}$=($\frac{5}{2}$cosθ+$\frac{5}{2}$,$\frac{5}{2}$sinθ)
∵$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$
∴($\frac{5}{2}$cosθ+$\frac{5}{2}$,$\frac{5}{2}$sinθ)=x($\frac{9}{5}$,$\frac{12}{5}$)+y(5,0)=($\frac{9}{5}$x+5y,$\frac{12}{5}$x)
∴$\frac{5}{2}$cosθ+$\frac{5}{2}$=$\frac{9}{5}$x+5y,$\frac{5}{2}$sinθ=$\frac{12}{5}$x,
∴y=$\frac{1}{2}$cosθ-$\frac{3}{8}$sinθ+$\frac{1}{2}$,x=$\frac{25}{24}$sinθ,
∴x+y=$\frac{1}{2}$cosθ+$\frac{2}{3}$sinθ+$\frac{1}{2}$=$\frac{5}{6}$sin(θ+φ)+$\frac{1}{2}$,其中sinφ=$\frac{3}{5}$,cosφ=$\frac{4}{5}$,
当sin(θ+φ)=1时,x+y有最大值,最大值为$\frac{5}{6}$+$\frac{1}{2}$=$\frac{4}{3}$,
故选:B
点评 本题考查了向量的坐标运算和向量的数乘运算和正弦函数的图象和性质,以及直角三角形的问题,考查了学生的分析解决问题的能力,属于难题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
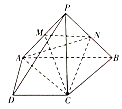 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8+4$\sqrt{3}$ | B. | 8-4$\sqrt{3}$ | C. | 12 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数大于等于120分 | 分数不足120分 | 合 计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合 计 | 25 | 20 | 45 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2e) | B. | (0,e) | C. | (0,1) | D. | (0,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com