
| A. | (0,2e) | B. | (0,e) | C. | (0,1) | D. | (0,$\frac{1}{e}$) |
分析 由函数图象的对称性可得f(x)-f(-x)在(0,+∞)上有两解,分离参数得-m=xlnx,求出右侧函数的单调性和极值即可得出m的范围.
解答 解:∵f(x)-f(-x)=0有四个不同的根,
且y=f(x)与y=f(-x)的图象关于y轴对称,
∴f(x)=f(-x)在(0,+∞)上有2解,
即lnx=-$\frac{m}{x}$有2解,∴-m=xlnx有2解,
令g(x)=xlnx,则g′(x)=lnx+1,
∴当0<x$<\frac{1}{e}$时,g′(x)<0,当x>$\frac{1}{e}$时,g′(x)>0,
∴g(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增,
当x=$\frac{1}{e}$时,f(x)取得极小值f($\frac{1}{e}$)=-$\frac{1}{e}$.
作出g(x)的大致函数图象如图所示: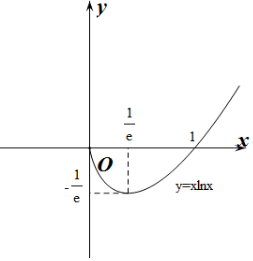
∵-m=xlnx有两解,
∴-$\frac{1}{e}$<-m<0,即0<m<$\frac{1}{e}$.
故选D.
点评 本题考查方程的根与函数的图象的关系,函数单调性判断与极值计算,属于中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{17}}}{6}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x与y正相关 | |
| B. | x与y具有较强的线性相关关系 | |
| C. | x与y几乎不具有线性相关关系 | |
| D. | x与y的线性相关关系还需进一步确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{1}{8}$ | B. | $x=\frac{1}{2}$ | C. | $x=-\frac{1}{8}$ | D. | $x=-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{3\root{3}{2}}{2}$ | C. | 2 | D. | $\root{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com