
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
分析 分别判定命题p、q的真假,再根据复合命题真假的真值表判定即可.
解答 解:满足条件的正方形ABCD,如下图示: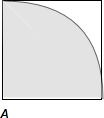
其中满足动点M到定点A的距离|MA|≤1的平面区域如图中阴影所示:
则正方形的面积S正方形=1阴影部分的面积为$\frac{π}{4}$,
故动点P到定点A的距离|MA|≤1的概率P=$\frac{π}{4}$.
故命题p为真命题.
对于函数f(x)=x+$\frac{4}{x}$,x∈[1,2),
则f′(x)=1-$\frac{4}{{x}^{2}}$=$\frac{(x+2)(x-2)}{{x}^{2}}$<0,
则f(x)在区间[1,2)上单调递减,
f(x)>f(2)=4,故命题q为假命题.
所以:p∧q为假命题;¬p假命题;p∧(¬q)是真命题;(¬p)∧(¬q)是假命题;
故选:C.
点评 本题考查了复合命题真假的判定,解题的关键是要把每个命题的真假给与正确判断,属于中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
 已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.
已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $sin({2x-\frac{π}{6}})$ | B. | $sin({2x+\frac{π}{3}})$ | C. | sin2x | D. | cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{17}}}{6}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com