
 已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.
已知圆O:x2+y2=r2,直线$x+2\sqrt{2}y+2=0$与圆O相切,且直线l:y=kx+m与椭圆C:$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点,O为原点.分析 (1)由直线与圆相切可求得圆的半径,由∠AOB=60°可得圆心到直线的距离,由此可得直线斜率,即可求解直线方程.
(2)设P(x1,y1),Q(x2,y2)
由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=kx+m\end{array}\right.$得(1+2k2)x2+4kmx+2m2-2=0,由△>0,得2k2+1>m2…(※),
由△POQ重心($\frac{{x}_{1}+{x}_{2}}{3}$,$\frac{{y}_{1}+{y}_{2}}{3}$)恰好在圆${x^2}+{y^2}=\frac{4}{9}$上,得${({x_1}+{x_2})^2}+{({y_1}+{y_2})^2}=4$,
化简得${m^2}=\frac{{{{(1+2{k^2})}^2}}}{{4{k^2}+1}}$,代入(※)得k≠0,即${m^2}=\frac{{{{(1+2{k^2})}^2}}}{{4{k^2}+1}}=1+\frac{{4{k^4}}}{{4{k^2}+1}}=1+\frac{4}{{\frac{4}{k^2}+\frac{1}{k^4}}}$
由k≠0,求出m的范围
解答 解:(1)因为直线$x+2\sqrt{2}y+2=0$与圆O:x2+y2=r2相切
∴$r=\frac{|0+0+2|}{{\sqrt{{1^2}+{{(2\sqrt{2})}^2}}}}=\frac{2}{3}$∴${x^2}+{y^2}=\frac{4}{9}$
因为左焦点坐标为F(-1,0),设直线l的方程为y=k(x+1)
由∠AOB=60°得,圆心O到直线l的距离$d=\frac{1}{{\sqrt{3}}}$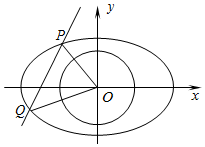
又$d=\frac{|k|}{{\sqrt{{k^2}+1}}}$,∴$\frac{|k|}{{\sqrt{{k^2}+1}}}=\frac{1}{{\sqrt{3}}}$,解得,$k=±\frac{{\sqrt{2}}}{2}$
∴直线l的方程为$y=±\frac{{\sqrt{2}}}{2}(x+1)$
(2)设P(x1,y1),Q(x2,y2)
由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=kx+m\end{array}\right.$得(1+2k2)x2+4kmx+2m2-2=0
由△>0,得2k2+1>m2…(※),
且${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}$
由△POQ重心($\frac{{x}_{1}+{x}_{2}}{3}$,$\frac{{y}_{1}+{y}_{2}}{3}$)恰好在圆${x^2}+{y^2}=\frac{4}{9}$上,得${({x_1}+{x_2})^2}+{({y_1}+{y_2})^2}=4$,
即${({x_1}+{x_2})^2}+{[k({x_1}+{x_2})+2m]^2}=4$,
即$(1+{k^2}){({x_1}+{x_2})^2}+4km({x_1}+{x_2})+4{m^2}=4$.
∴$\frac{{16(1+{k^2}){k^2}{m^2}}}{{{{(1+2{k^2})}^2}}}-\frac{{16{k^2}{m^2}}}{{1+2{k^2}}}+4{m^2}=4$,
化简得${m^2}=\frac{{{{(1+2{k^2})}^2}}}{{4{k^2}+1}}$,代入(※)得k≠0
又${m^2}=\frac{{{{(1+2{k^2})}^2}}}{{4{k^2}+1}}=1+\frac{{4{k^4}}}{{4{k^2}+1}}=1+\frac{4}{{\frac{4}{k^2}+\frac{1}{k^4}}}$
由k≠0,得$\frac{1}{k^2}>0$,∴$\frac{4}{k^2}+\frac{1}{k^4}>0$,
∴m2>1,得m的取值范围为m<-1或m>1
点评 本题考查了椭圆 与直线的位置关系,方程思想、转化思想,运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
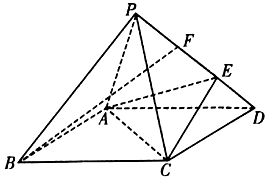 19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.
19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
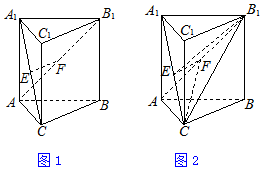 如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1与底面垂直,∠ACB=90°,AC=BC,AA1=AB=2,E,F分别是A1C,AB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
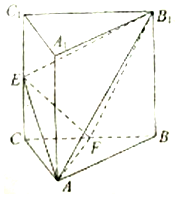 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,E,F分别是CC1,BC的中点,且AB=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
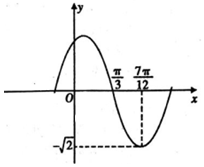 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | B. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
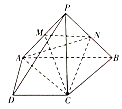 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com