
 ,
,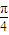 ),直线l过点P,且倾斜角为
),直线l过点P,且倾斜角为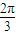 ,方程
,方程 =1所对应的曲线经过伸缩变换
=1所对应的曲线经过伸缩变换 后的图形为曲线C.
后的图形为曲线C. ,可得直线l的参数方程;确定坐标之间的关系,代入方程,化简可得结论;
,可得直线l的参数方程;确定坐标之间的关系,代入方程,化简可得结论;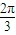 ,∴直线l的参数方程为
,∴直线l的参数方程为 (t为参数)
(t为参数)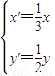 ,∴
,∴
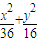 =1,可得
=1,可得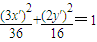 ,即x′2+y′2=4
,即x′2+y′2=4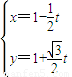 ,代入曲线C可得t2+(
,代入曲线C可得t2+( )t-2=0
)t-2=0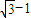 ;t1t2=-2
;t1t2=-2

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
| 2π |
| 3 |
| x2 |
| 36 |
| y2 |
| 16 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| π |
| 2 |
| π |
| 3 |
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com