
分析 (1)通过代入f(x)=$\frac{2}{3}$+$\frac{1}{x}$(x>0)可知数列{an}是首项为1、公差为$\frac{2}{3}$的等差数列,进而计算可得结论;
(2)通过(1)裂项可知$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{9}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),进而并项相加可知Sn=$\frac{3n}{2n+3}$,从而问题转化为求$\frac{4{n}^{2}}{2n+3}$的最小值,通过利用导数可知g(x)=$\frac{4{x}^{2}}{2x+3}$(x>0)的单调性,计算即得结论.
解答 解:(1)∵f(x)=$\frac{2}{3}$+$\frac{1}{x}$(x>0),an=f($\frac{1}{{a}_{n-1}}$),
∴an+1-an=$\frac{2}{3}$,
又∵a1=1,
∴数列{an}是首项为1、公差为$\frac{2}{3}$的等差数列,
∴其通项公式an=1+(n-1)$\frac{2}{3}$=$\frac{2n+1}{3}$;
(2)由(1)可知:$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{9}{(2n+1)(2n+3)}$=$\frac{9}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
∴Sn=$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…+$\frac{1}{{a}_{n}{a}_{n-1}}$
=$\frac{9}{2}$[($\frac{1}{3}$-$\frac{1}{5}$)+($\frac{1}{5}$-$\frac{1}{7}$)+…+($\frac{1}{2n+1}$-$\frac{1}{2n+3}$)]
=$\frac{9}{2}$($\frac{1}{3}$-$\frac{1}{2n+3}$)
=$\frac{3n}{2n+3}$,
则Sn≥$\frac{3t}{4n}$恒成立等价于$\frac{3n}{2n+3}$≥$\frac{3t}{4n}$,即t≤$\frac{4{n}^{2}}{2n+3}$恒成立,
令g(x)=$\frac{4{x}^{2}}{2x+3}$(x>0),则g′(x)=$\frac{8x(x+3)}{(2x+3)^{2}}$>0,
∴函数g(x)=$\frac{4{x}^{2}}{2x+3}$(x>0)为增函数,
∵当n=1时$(\frac{4{n}^{2}}{2n+3})_{min}$=$\frac{4}{5}$,
∴t≤$\frac{4}{5}$,即实数t的取值范围是:(-∞,$\frac{4}{5}$].
点评 本题是一道关于数列与不等式的综合题,涉及裂项相消法,利用导数研究函数的单调性等基础知识,注意解题方法的积累,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
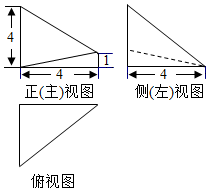 已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )
已知某几何体的三视图(如图),其中俯视图和侧(左)视图都是腰长为4的等腰直角三角形,正(主)视图为直角梯形,则此几何体的体积V的大小为( )| A. | $\frac{35}{3}$ | B. | 12 | C. | 16 | D. | $\frac{40}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 23 | C. | 32 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com