
已知A,B 分别为曲线C: ![]() +
+![]() =1(y
=1(y![]() 0,a>0)与x轴的左、右两个交点,直线
0,a>0)与x轴的左、右两个交点,直线![]() 过点B,且与
过点B,且与![]() 轴垂直,S为
轴垂直,S为![]() 上异于点B的一点,连结AS交曲线C于点T.
上异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧![]() 的三等分点,试求出点S的坐标;
的三等分点,试求出点S的坐标;
(II)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在![]() ,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。w.w
,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。w.w
.w.k .s.5.u.c.o.m
.s.5.u.c.o.m ![]()
![]()
⑴![]() ⑵存在
⑵存在![]() ,使得O,M,S三点共线.
,使得O,M,S三点共线.
解法二:
解法一:
(Ⅰ)当曲线C为半圆时,![]() 如图,由点T为圆弧
如图,由点T为圆弧![]() 的三等分点得∠BOT=60°或120°.
的三等分点得∠BOT=60°或120°.
(1)当∠BOT=60°时, ∠SAE=30°.
又AB=2,故在△SAE中,有![]()
(2)当∠BOT=120°时,同理可求得点S的坐标为![]() ,综上,
,综上, ![]()
(Ⅱ)假设存在![]() ,使得O,M,S三点共线.
,使得O,M,S三点共线.
由于点M在以SB为直线的圆上,故![]() .
.
显然,直线AS的斜率k存在且k>0,可设直线AS的方程为![]() .
.
由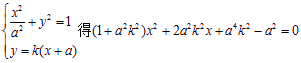
设点![]()
故![]() ,从而
,从而![]() .
.
亦即![]()
![]()
由![]() 得
得![]()
由![]() ,可得
,可得![]() 即
即![]()
![]()
经检验,当![]() 时,O,M,S三点共线. 故存在
时,O,M,S三点共线. 故存在![]() ,使得O,M,S三点共线.
,使得O,M,S三点共线.
解法二:
(Ⅰ)同解法一.
(Ⅱ)假设存在a,使得O,M,S三点共线.
由于点M在以SO为直径的圆上,故![]() .
.
显然,直线AS的斜率k存在且K>0,可设直线AS的方程为![]()
由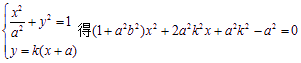
设点![]() ,则有
,则有![]()
故![]()
![]()
由![]() 所直线SM的方程为
所直线SM的方程为![]()
O,S,M三点共线当且仅当O在直线SM上,即![]() .
.
![]()
故存在![]() ,使得O,M,S三点共线.
,使得O,M,S三点共线.


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| FB |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2010年福建省高二第二学期半期考试数学(理科)试题 题型:解答题
(本小题满分14分)
如图所示,已知曲线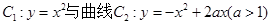 交于点O、A,直线
交于点O、A,直线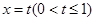 与曲线
与曲线 、
、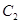 分别交于点D、B,连结OD,DA,AB.
分别交于点D、B,连结OD,DA,AB.
(1)求证:曲边四边形ABOD(阴影部分:OB为抛物线弧)的面积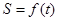 的函数表达式为
的函数表达式为 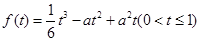

(2)求函数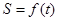 在区间
在区间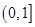 上的最大值.
上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com