
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销量价格P(元)的关系如图所示;③每月需各种开支2 000元.
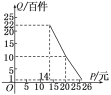
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
科目:高中数学 来源: 题型:
【题目】某地自来水苯超标,当地自来水公司对水质检测后,决定在水中投放一种药剂来净化水质,已知每投放质量为![]() 的药剂后,经过
的药剂后,经过![]() 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度![]() (毫克/升)满足
(毫克/升)满足![]() ,其中
,其中 ,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(Ⅰ)如果投放的药剂质量为![]() ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(Ⅱ)如果投放的药剂质量为![]() ,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:

(Ⅰ)求频率分布直方图中![]() 的值;
的值;
(Ⅱ)分别求出成绩落在![]() ,
, ![]() 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是( )
A.多于4个 B.4个
C.3个 D.2个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数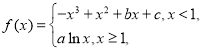 图象过点
图象过点![]() ,且在该点处的切线与直线
,且在该点处的切线与直线![]() 垂直.
垂直.
(1)求实数![]() ,
,![]() 的值;
的值;
(2)对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在![]() 轴上?
轴上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com