
已知函数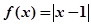 .
.
(1)用分段函数的形式表示该函数;
(2)在右边所给的坐标系中画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间(不要求证明).

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源:2015届河北邢台一中高一上学期第三次月考数学试卷(解析版) 题型:解答题
(本题满分12分)
已知函数 ,
,
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)求单调增减区间。

查看答案和解析>>
科目:高中数学 来源:2015届云南大理州宾川第四高级中学高一11月月考数学试卷(解析版) 题型:解答题
(本小题满分15分)已知函数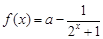 ,
,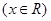 .
.
(1)用定义证明:不论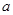 为何实数
为何实数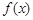 在
在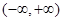 上为增函数;
上为增函数;
(2)若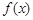 为奇函数,求
为奇函数,求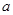 的值;
的值;
(3)在(2)的条件下,求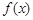 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届福建省三明市高一第一次段考数学试卷(解析版) 题型:解答题
已知函数 ,
, .
.
(1)用定义证明:不论 为何实数
为何实数 在
在 上为增函数;
上为增函数;
(2)若 为奇函数,求
为奇函数,求 的值;
的值;
(3)在(2)的条件下,求 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年福建省四地六校联考高一第三次月考数学卷 题型:解答题
(本题13分)
已知函数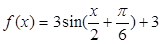 ,
,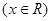

(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由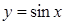 ,
,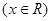 的图象经怎样的变换得到.
的图象经怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源:2010-2011年内蒙古赤峰市高一下学期第一次月考考试数学试卷 题型:解答题
(12分)已知函数 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
 (3)说明此函数图象可由
(3)说明此函数图象可由 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com